Supervised Machine Learning

Foundations

Learning

The ability to improve behaviour based on experience

• The range of behaviour is expanded
  • the agent can do more
• The accuracy on tasks is improved
  • the agent can do things better
• The speed is improved
  • the agent can do things faster

Components of a Learning Problem

The following component are part of any learning problem:

• Task:
  • The behaviour or task that’s being improved
  • E.g. classification, acting in an environment
• Data:
  • The experiences that are being used to improve performance in the task
• Measure of improvement
  • How can the improvement be measured?
  • E.g. increasing accuracy in prediction, new skills that were not present initially, improved speed

Types of Learning

• Deduction
  • Top-down
  • Make a prediction from a knowledge base
• Induction
  • Bottom-up
  • Infer laws from data
• Abduction
  • Infer causes from experience and knowledge
• The richer and more complex the representation, the more useful it is for subsequent problem solving
  • The richer the representation, the more difficult it is to learn

Common Learning Tasks

• Supervised Classification
  • Given a set of pre-classified training examples, classify a new instance
• Unsupervised Learning
  • Find natural classes for examples
• Reinforcement Learning
  • Determine what to do based on rewards and punishments
• Transfer Learning
  • Learning from an expert
• Active Learning
  • Learner actively seeks to learn
• Inductive Logic Programming
  • Build richer models in terms of logic programs

Feedback

Learning Tasks can be characterized by the feedback given to the learner

• Supervised Learning
  • What has to be learned is specified for each example
• Unsupervised Learning
  • No classifications are given
  • The learner has to discover the categories and regularities in the data
• Reinforcement Learning
  • Feedback occurs after a sequence of actions

Measuring Success

The measure of success is not how well the agent performs on the training examples, but how well the agent performs for new (unseen) examples

• Consider two agents solving a binary classification task:
  • P claims that negative examples seen are the only negative examples
    • Every other instance is positive
  • N claims the positive examples seen are the only positive examples
    • Every other instance is negative
• Both agents correctly classify every training example, but disagree on every other example

Bias

The tendency to prefer one hypothesis over another is called a bias

• A bias is necessary to make predictions on unseen data
• Saying a hypothesis is better than $N$’s or $P$’s hypothesis isn’t something that’s obtained from the data
• To have any inductive process make predictions on unseen data, you need a bias
• What constitutes a good bias is an empirical question about which biases work best in practice

Learning as Search

• Given a representation and a bias, the problem of learning can be reduced to one of search
  • Learning is search through the space of possible representations look for the representation or representations that best fits the data, given the bias
  • These search spaces are typically prohibitively large for systematic search
  • A learning algorithm is made of a search space, an evaluation function, and a search method

Supervised Learning

Given:

• a set of input features $X_1,\cdots ,X_n$
• a set of target features $Y_1,\cdots ,Y_n$
• a set of training examples where the values for the input features and the target features are given for each example
• a set of test examples, where only the values for the input features are given
  Predict the values for the target features for the test examples
• classification when the $Y_i$ are discrete
• regression when the $Y_i$ are continuous
  Very important: keep training and test sets separate

Noise

Data isn’t perfect

• Some of the features are assigned the wrong value
• The features given are inadequate to predict the classification
• There are examples with missing features
  Overfitting occurs when a distinction appears in the data, but doesn’t appear in the unseen examples
• this occurs because of random correlations in the training set

Evaluating Predictions

Suppose $Y$ is a feature and $e$ is an example:

• $Y(e)$ is the value of feature $Y$ for example $e$
• $\hat{Y}(e)$ is the predicted value of feature $Y$ for example $e$
• The error of the prediction is a measure of how close $\hat{Y}(e)$ is to $Y(e)$
• There are many possible errors that could be measured

Measure of Error

$E$ is the set of examples. $T$ is the set of target features

• Absolute Error

• Sum of Square Error

• Worst-case Error

• A cost-based error takes into account costs of various errors

Precision and Recall

Not all errors are equal, e.g. predict:

• a patient has a disease when they do not
• a patient doesn't have a disease when they do
  Need to map out both kinds of errors to find the best trade-off
  
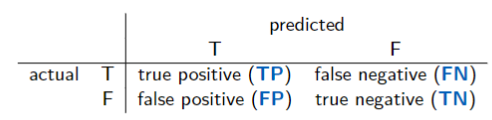
• recall = sensitivity = TP/(TP+FN)
• specificity = TN/(TN+FP)
• precision = TP/(TP+FP)
• F1-measure = $\frac{2\times Precision\times Recall}{Precision+Recall}$
  • gives even weight to precision and recall

Receiver Operating Curve (ROC)

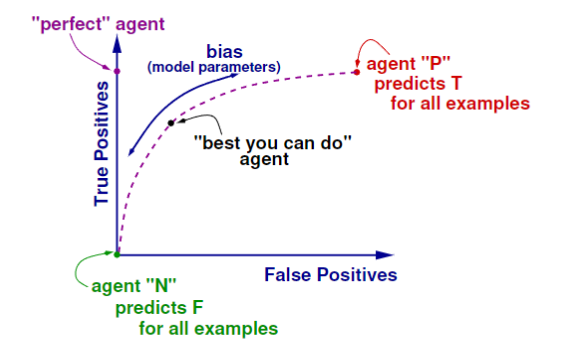
The ROC gives full range of performance of an algorithm across different biases

Basic Models for Supervised Learning

Many learning algorithms can be seen as deriving from:

• decision trees
• linear classifiers
  • neural networks
• Bayesian Classifiers

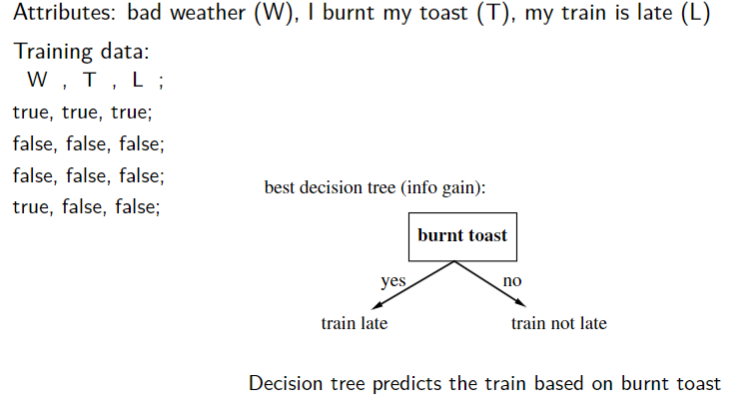
Decision Trees

Simple, successful technique for supervised learning from discrete data

• Representation is a decision tree
• Bias is towards simple decision trees
• Search through the space of decision trees, from simple decision trees to more complex ones

Properties of Decision Tree

• Nodes are input attribute/features
• Branches are labelled with input feature value
  • Branches can be labelled with multiple feature values
• Leaves are predictions for target features
  • point estimates
• Can have many branches per node

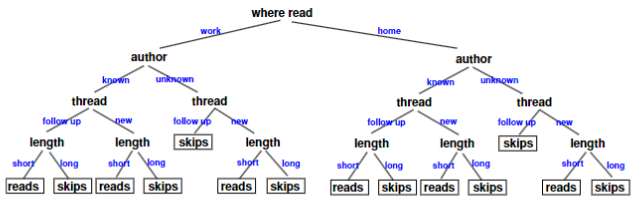
Examples

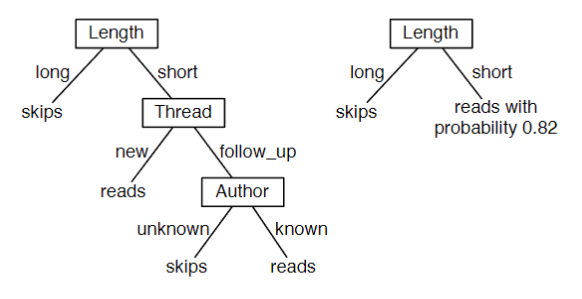
Learning a Decision Tree

• Incrementally split the training data
• Recursively solve sub-problems
• Hard part: how to split the data?
• Criteria for good decision tree (bias):
  • small decision tree
  • good classification
    • low error on training data
  • good generalisation
    • low error on test data

Pseudocode

Remaining Issues

• Stopping criteria
• Selection of features
• Point estimate
  • final return value at leaf
• Reducing number of branches
  • Partition of domain for N-ary features

Stopping Criteria

How do we decide to stop splitting?

• The stopping criteria is related to the final return value
• Depends on what we will need to do
• Possible stopping criteria:
  • No more features
  • Performance on training data is good enough

Feature Selection

Ideal: choose sequence of features that result in smallest tree
Actual: myopically split

• as if only allowed one split, which feature would give best performance?
  Heuristics for best performing feature:
• Most even split
• Maximum information gain
• GINI index
• … others domain dependent …

Good Feature Selection

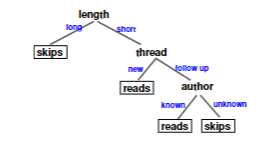
Bad Feature Selection

Information Theory

• a bit is a binary digit: 0 or 1
• n bits can distinguish $2^n$ items
• can do better by taking probabilities into account

In general, need $-{\log }_{2}P(x)$ bits to encode $x$

• Each symbol requires on average $-P(x){\log }_{2}P(x)$ bits
• To transmit an entire sequence distributed according to $P(x)$, we need on average
  • $\sum _x-P(x){\log }_{2}P(x)$ bits of information per symbol we wish to transmit
• information content or entropy of the sequence

Information Gain

Given a set $E$ of $N$ training examples, if the number of examples with output feature $Y=y_i$ is $N_i$, then $$P(Y=y_i)=P(y_i)=\frac{N_i}{N}$$(the point estimate)
Total information content for the set $E$ is $$I(E)=-\sum_{y_i\in Y}P(y_i)\log_2P(y_i)$$
So, after splitting $E$ up into $E_1$ and $E_2$ with size $N_1,N_2$ based on input attribute $X_i$, the information content $$I(E_{split}) = \frac{N_1}{N}I(E_1) + \frac{N_2}{N}I(E_2)$$
and we want the $X_i$ that maximizes the information gain:$$I(E)-I(E_{split})$$
Information gain is always non-negative:

• Intuitively, information gain is the reduction in uncertainty about the output feature $Y$ given the value of a certain input feature $X$

Final Return Value

Point estimate of $Y$ (output features) over all examples

• Point estimate is just a prediction of target features
  • mean value,
  • median value,
  • most likely classificaiton
  • etc.
• e.g. $$P(Y=y_i) = \frac{N_i}{N}$$where
  • $N_i$ is the number of training samples at the leaf with $Y=Y_i$
  • $N$ is the total number of training samples at the leaf

Using a Priority Queue to Learn the DT

Some branches might be more worthwhile to expand
Idea: sort the leaves using a priority queue ranked by how much information can be gained with the best feature at the leaf

• Always expand the leaf at the top of the queue

Pseudocode

Overfitting

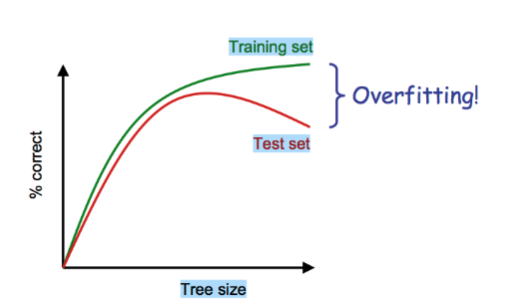
Sometimes the decision tree is too good at classifying the training data, and will not generalise very well.

• This often occurs when there is not much data

Some methods to avoid overfitting:

• Regularization
  • e.g. Prefer small decision trees over big ones
    • add a “complexity” penalty to the stopping criteria
    • stop early
• Pseudocounts:
  • add some data based on prior knowledge
• Cross Validation

Test set errors caused by:

• bias:
  • the error due to the algorithm finding an imperfect model
  • representation bias: model is too simple
  • search bias: not enough search
• variance: the error is due to lack of data
• noise: the error due to the data depending on features not modeled
  • or because the process generating the data is inherently stochastic
• bias-variance trade-off:
  • Complicated model, not enough data
    • low bias, high variance
  • Simple model, lots of data
    • high bias, low variance
      
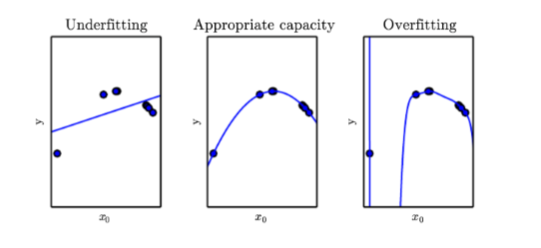
      Capacity of a model is its ability to fit a wide variety of functions
• capacity is like the inverse of bias
  • high capacity model has low bias and vice-versa

Cross Validation

Split training data into a training and a validation set

• Use the validation set as a ”pretend” test set
• Optimise the decision maker to perform well on the validation set
  • not the training set
• Can do this multiple times with different validation sets