Probability and Bayesian Networks

Uncertainty

Why is uncertainty important?

• Agents and humans don’t know everything
  • but need to make decisions anyways!
• Decisions are made in the absence of information
  The best an agent can do:
• Know how uncertain it is, and act accordingly

Probability

Frequentist vs. Bayesian

Frequentist view:

• Probability of heads = # of heads / # of flips
• probability of heads this time = probability of heads (history)
• Uncertainty is ontological:
  • pertaining to the world

Bayesian view:

• Probability of heads this time = agent’s belief about flip
• Belief of agent A:
  • based on previous experience of agent A
• Uncertainty is epistemological:
  • pertaining to knowledge

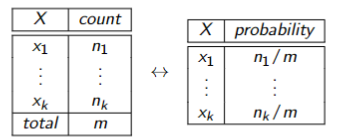
Probability Measure

If $X$ is a random variable (feature, attribute)

• it can take on values $x$, where $x\in Domain(X)$
• assume $x$ is discrete
  $P(X)$ is the probability that $X=x$
  Joint probability $P(x,y)$ is the probability that $X=x$ and $Y=y$ at the same time

Axioms of Probability

Axioms are things we have to assume about probability

• $P(X)\ge 0$
• $\sum _{x}P(X=x)=1.0$
• $P(a\vee b)=P(a)+P(b)$ if $a$ and $b$ are contradictory
  • can’t both be true at the same time
  • $P(win\vee lose)=P(win)+P(lose)=1.0$
    Some notes:
• probability between 0-1 is purely convention
• $P(a)=0$ means you think a is definitely false
• $P(a)=1$ means you think a is definitely true
• $0<P(a)<1$ means you have belief about the truth of $a$
  • It does not mean that $a$ is true to some degree, just that you are ignorant of its truth value
• Probability = measure of ignorance

Independence

Describe a system with $n$ features: $2^{n-1}$ probabilities

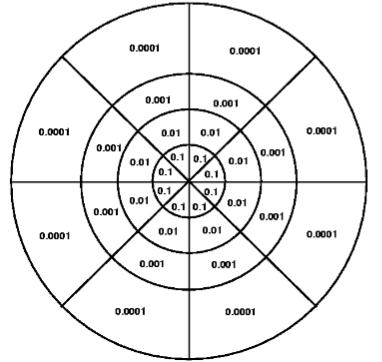
• Use independence to reduce number of probabilities
  • e.g. radially symmetric dartboard, P(hit a sector)
    • $P(sector)=P(r,\theta )$ where $r=1,\cdots ,4$ and $\theta =1,\cdots ,8$
    • 32 sectors in total - need to give 31 numbers
  • Assume radial independence: $P(r,\theta )=P(r)P(\theta )$
    • only need 7 + 3 = 10 numbers
      
      

Conditional Probability

If $X$ and $Y$ are random variables, the

• $P(x|y)$ is the probability that $X=x$ given that $Y=y$
  Incorporate Independence:
• $P(flies|is\mathrm{\_}bird,has\mathrm{\_}feathers)=P(flies|is\mathrm{\_}bird)$
  • assuming all birds have feathers
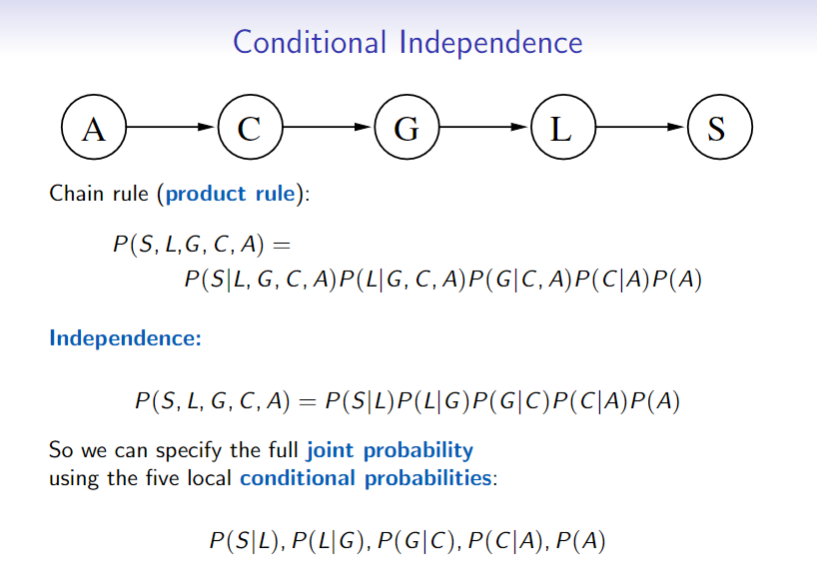
    Product Rule (Chain Rule):
• $P(flies,is\mathrm{\_}bird)=P(flies|is\mathrm{\_}bird)P(is\mathrm{\_}bird)=P(is\mathrm{\_}bird|flies)P(flies)$
  Leads to: Bayes’ Rule

Sum Rule

We know

• $\sum _{x}P(X=x)=1.0$ and therefore that $\sum _{x}P(X=x|Y)=1.0$
  This means that (Sum Rule)

We call $P(Y)$ the marginal distribution over $Y$

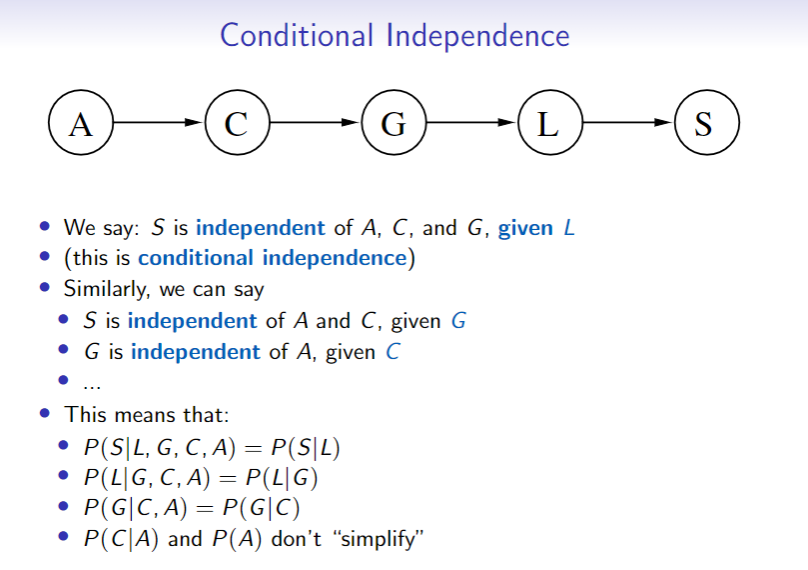
Conditional Independence

$X$ and $Y$ are independent iff

• $P(X)=P(X|Y)$
• $P(Y)=P(Y|X)$
• $P(X,Y)=P(X)P(Y)$
• So learning $Y$ doesn’t influence beliefs about $X$
  $X$ and $Y$ are conditionally independent give $Z$ iff
• $P(X|Z)=P(X|Y,Z)$
• $P(Y|Z)=P(Y|X,Z)$
• $P(X,Y|Z)=P(X|Z)P(Y|Z)$
• So learning $Y$ doesn’t influence beliefs about $X$ if you already know $Z$
  • does not mean $X$ and $Y$ are independent

Expected Values

Expected value of a function on $X$, $V(X)$:

where $P(x)$ is the probability of $X=x$
This is useful in decision making

• where $V(X)$ is the utility of situation $X$
  Bayesian decision making is then

Value of Independence

• Complete independence reduces both representation and influence from $O(2^n)$ to $O(n)$
• Unfortunately, complete mutual independence is rare
• Fortunately, most domains do exhibit a fair amount of conditional independence
• Bayesian Networks or Belief Networks encode this information

Bayesian Networks

Bayesian Networks or Belief Networks

• Directed Acyclic Graph
• Encodes independencies in a graphical format
• Edges give $P(X_i|parents(X_i))$

Example

Correlation and Causality

Directed links in Bayes’ net $\approx$ causal

• However, not always the case
  In a Bayes net, it doesn’t matter
• But, some structures will be easier to specify

Example

A Bayesian Network or BN over variables $\{X_1,X_2,\cdots ,X_N\}$ consists of:

• a DAG whose nodes are the variables
• a set of Conditional Probability Tables (CPTs) giving $P(X_i|Parents(X_i))$ for each $X_i$
  Example probability tables for the Coffee Bayes Net:
  

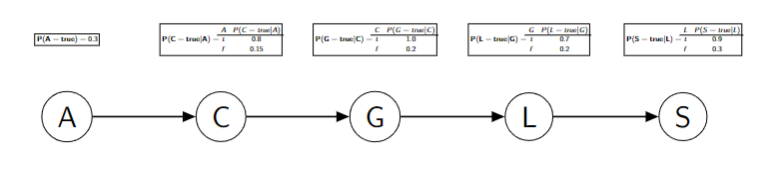
Semantics of a Bayes’ Net

The BN defines a factorization of the joint probability distribution

• The joint distribution is formed by multiplying the conditional probability tables together

Constructing Belief Networks

To represent a domain in a belief network, you need to consider:

• What are the relevant variables?
  • What will you observe?
    • this is the evidence
  • What would you like to find out?
    • this is the query
  • What other features make the model simpler?
    • these are the other variables
• What values should these variables take?
• What is the relationship between them?
  • this should be expressed in terms of local influence
• How does the value of each variable depend on its parents?
  • this is expressed in terms of the conditional probabilities

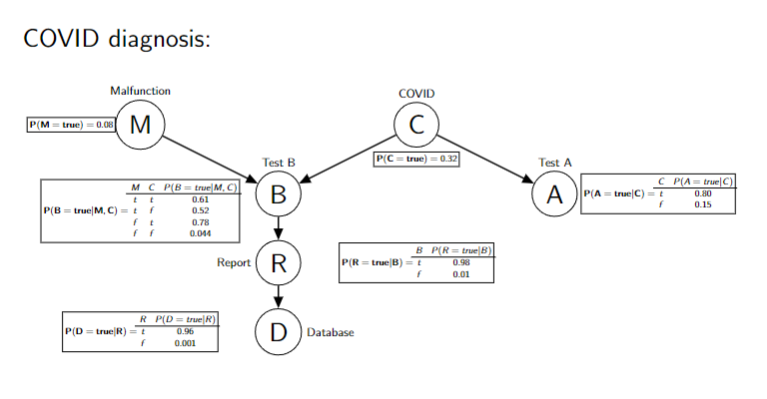
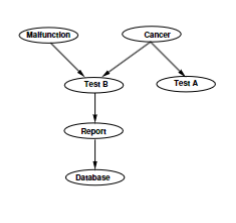
Three Basic Bayesian Networks

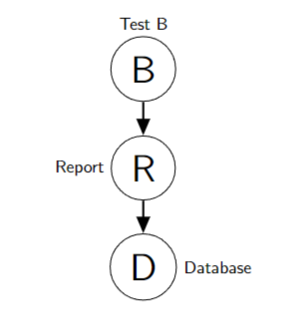
• Database and Test B independent if Report is observed
  
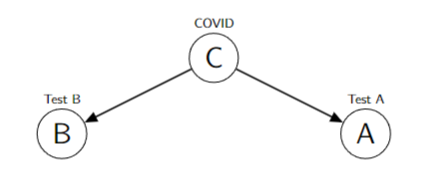
• Test B and Test A independent if COVID is observed
  
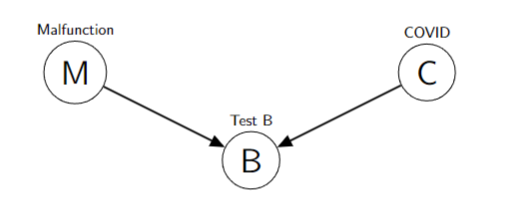
• Malfunction and COVID are independent if Test B is not observed

Updating Belief: Bayes’ Rule

Agent has a prior belief in a hypothesis, $h,P(h)$

• Agent observes some evidence $e$ that has a likelihood given the hypothesis: $P(e|h)$
  The agent’s posterior belief about $h$ after observing $e, $P(h|e)$ is given by Bayes’ Rule:

• Useful when we have causal knowledge and want to do evidential reasoning

Probabilistic Inference

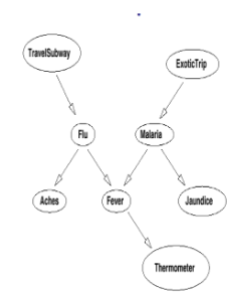
Simple Forward Inference (Chain)

Computing marginal requires simple forward propagation of probabilities

• $P(B)=\sum _{m,c}P(M=m,C=c,B)$
  • marginalization - sum rule
• $P(B)=\sum _{m,c}P(B|m,c)P(m|c)P(c)$
  • chain rule
• $P(B)=\sum _{m,c}P(B|m,c)P(m)P(c)$
  • independence
• $P(B)=\sum _{m}P(m)\sum _{c}P(c)P(B|m,c)$
  • distribution of product over sum

Same idea when evidence $COVID=true$ “upstream”

• $P(R|c)=\sum _{m,b}P(R,b,m|c)$
  • marginalization
• $P(R|c)=\sum _{m,b}P(R|b,m,c)P(b|m,c)P(m|c)$
  • chain rule
• $P(R|c)=\sum _{m,b}P(R|b)P(b|m,c)P(m)$
  • independence and conditional independence

With multiple parents the evidence is “pooled”

Also works with “upstream” evidence

Simple Backward Inference

When evidence is downstream of query, then we must reason “backwards”.

• This requires Bayes’ rule
  

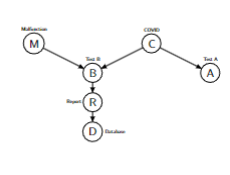
Normalizing constant is $\frac{1}{P(r)}$, but this can be computed as $$P(r) = \sum_bP(r, b)$$

Variable Elimination

More general algorithm:

• applies sum-out rule repeatedly
• distributes sums

Factors

a factor is a representation of a function from a tuple of random variables into a number

• We will write factor $f$ on variables $X_1,\cdots ,X_j$ as $f(X_1,\cdots ,X_j)$
• We can assign some or all of the variables of a factor
  • this is restricting a factor:
    • $f(X_1=v_1,X_2,\cdots ,X_j)$, where $v_1\in dom(X_1)$, is a factor on $X_2,\dots ,X_j$
    • $f(X_1=v_1,X_2=v_2,\cdots ,X_j=v_j)$ is a number that is the value of $f$ when each $X_i$ has value $v_i$
      The former is also written as $f(X_1,X_2,\cdots ,X_j{)}_{X_1=v_1}$, etc.

Multiplying Factors

The product of factor $f_1(X,Y)$ and $f_2(Y,Z)$, where $Y$ are the variables in common, is the factor $(f_1\times f_2)(X,Y,Z)$ defined by:

Summing out variables

We can sum out a variable, say $X_1$ with domain $\{v_1,\cdots ,v_k\}$, from factor $f(X_1,\cdots ,X_j)$, resulting in a factor on $X_2,\cdots ,X_j$ defined by:

Evidence

If we want to compute the posterior probability of $Z$ given evidence $Y_1=v_1\wedge \cdots \wedge Y_j=v_j$:

The computation reduces to the joint probability of $P(Z,Y_1=v_1,\cdots ,Y_j=v_j)$, normalize at the end

• can also restrict the query variable
  • e.g. compute: $P(Z=z|Y_1=v_1,\cdots ,Y_j=v_j)$

Probability of a conjunction

Suppose the variables of the belief network are $X_1,\cdots ,X_n$

• To compute $P(Z,Y_1=v_1,\cdots ,Y_j=v_j)$, we sum out the variables other than query $Z$ and evidence $Y$
  • $Z_1,\cdots ,Z_k=\{X_1,\cdots ,X_n\}-\{Z\}-\{Y_1,\cdots ,Y_j\}$
• We order the $Z_i$ into an elimination ordering $Z_1,\cdots ,Z_k$

Computing sums of products

Computation in belief networks reduces to computing the sums of products

• How can we compute $ab+ac$ efficiently?
  • Distribute out the $a$ giving $a(b+c)$
• How can we compute $\sum _{Z_1}\prod _{i=1}^{n}P(X_i|parents(X_i))$ efficiently?
  • Distribute out those factors that don’t involve $Z_1$

Variable Elimination Algorithm

To compute $P(Z|Y_1=v_1\wedge \cdots \wedge Y_j=v_j)$:

• Construct a factor for each conditional probability
• Restrict the observed variables to their observed values
• Sum out each of the other variables according to some elimination ordering:
  • for each $Z_i$ in order starting from $i=1$:
    • collect all factors that contain $Z_i$
    • multiply together and sum out $Z_i$
    • add resulting new factor back to the pool
• Multiply the remaining factors
• Normalize by dividing the resulting factor $f(z)$ by $\sum _{Z}f(Z)$

Summing our a Variable

To sum out a variable $Z_j$ from a product $f_1,\cdots ,f_k$ of factors:

• Partition the factors into
  • those that don’t contain $Z_j$, say $f_1,\cdots ,f_i$,
  • those that contain $Z_j$, say $f_{i+1},\cdots ,f_k$
    We know:

• Explicitly construct a representation of the rightmost factor $(\sum _{Z_j}{f}_{i+1}\times \cdots \times f_k)$
• Replace the factors of $f_{i+1},\cdots ,f_k$ by the new factor

Notes on Variable Elimination

• Complexity is linear in number of variables, and exponential in the size of the largest factor
• When we create new factors: sometimes this blows up
• Depends on the elimination ordering
• For polytrees:
  • work outside in
• For general BNs this can be hard
• simply finding the optimal elimination ordering is NP-hard for general BNs
• inference in general is NP-hard

Variable Ordering

Polytrees

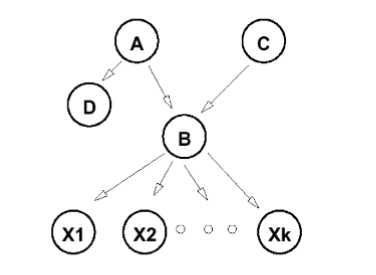
• eliminate singly-connected nodes $(D,A,C,X_1,\cdots ,X_k)$ first
• Then no factor is ever larger than original CPTs
  • if you eliminate $B$ first, a large factor is created that includes $A,B,C,X_1,\cdots ,X_k$

Relevance

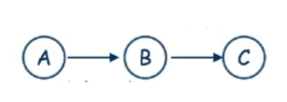
Certain variables have no impact

• In ABC network above, computing $P(A)$ does not require summing over $B$ and $C$
  
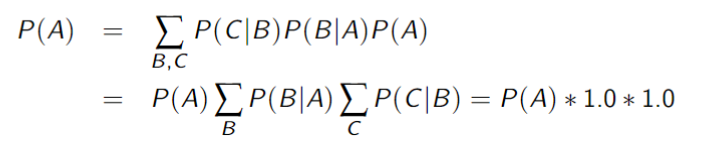
  Can restrict attention to relevant variables:
• Given query $Q$ and evidence $\mathbf{\text{E}}$, complete approximation is:
  • $Q$ is relevant
  • if any node is relevant, its parents are relevant
  • if $E\in \mathbf{\text{E}}$ is a descendent of a relevant variable, then $E$ is relevant
    Irrelevant variable: a node that is not an ancestor of a query or evidence variable
• This will only remove irrelevant variables, but may not remove them all

Probability and Time

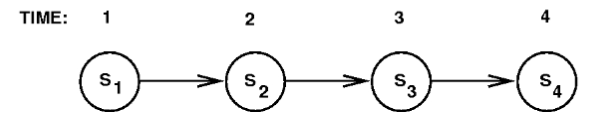
• A node repeats over time
• Explicit encoding of time
• chain has length = amount of time you want to model
• event-driven times or clock-driven times
  • e.g. Markov chain

Markov Assumption

$P(S_{t+1}|S_1,\cdots ,S_t)=P(S_{t+1}|S_t)$
This distribution gives the dynamics of the Markov Chain

Hidden Markov Models (HMMs)

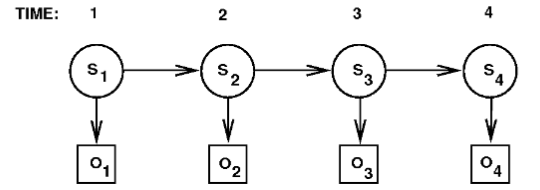
Add: observations $O_t$

• always observed, so the node is square
  Observation function $P(O_t|s_t)$
• Given a sequency of observations $O_1,\cdots ,O_t$, can estimate filtering:
  • $P(S_t|O_1,\cdots ,O_t)$
• Or smoothing, for $k>t$
  • $P(S_k|O_1,\cdots ,O_t)$

Speech Recognition

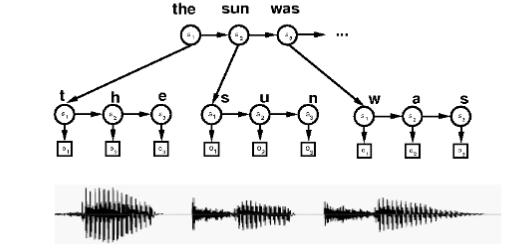
• Observations: audio features
• States: phonemes
• Dynamics: models
  • e.g. co-articulation
• HMMs: words
• Can build hierarchical models (e.g. sentences)

Dynamic Bayesian Networks (DBNs)

In general, any Bayesian network can repeat over time: DBN

• Many examples can be solved with variable elimination
• may become too complex with enough variables
• event-drive times or clock-driven times

Stochastic Simulation

Idea: probabilities $⟺$ samples

• Get probabilities from samples:
  • 
• If we could sample from a variable’s (posterior) probability, we could estimate its (posterior) probability

Generating Samples from a distribution

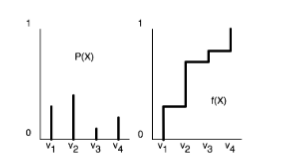
For a variable $X$ with a discrete domain or a one-dimensional real domain:

• Totally order the values of the domain of $X$
• Generate the cumulative probability distribution:
  • $f(x)=P(X\le x)$
• Select a value $y$ uniformly in the range $[0,1]$
• Select $x$ such that $f(x)=y$

Forward Sampling in a Belief Network

• Sample the variables one at a time;
• Sample parents of $X$ before you sample $X$
  • Given values for the parents of $X$, sample from the probability of $X$ given its parents
• for samples $s_i,i=1,\cdots ,N$:$$P(X=x_i)\propto \sum_{s_i}\delta(x_i)=N_{X=x_i}$$where $\delta (x_i)=1$ if $X=x_i$ in $s_i$ and 0 otherwise

Example

• A: 2/3 based on first 7 samples