Machine Learning
Bayesian Learning
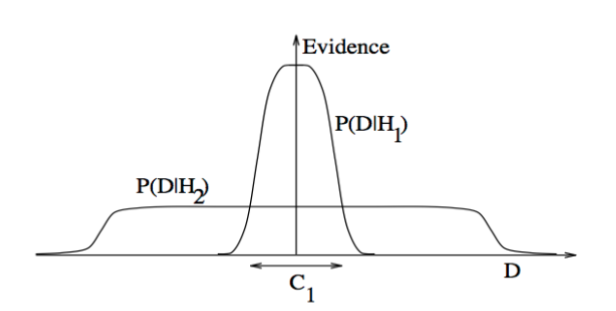
Basic premise:
- have a number of hypotheses or models
- don’t know which one is correct
- Bayesians assume all are correct to a certain degree
- Have a distribution over the models
- Compute expected prediction given this average
Suppose
- We sum over all models,
Bayesian Learning
- Prior:
- Likelihood:
- Evidence:
Bayesian Learning: Update the posterior (Bayes’ Theorem)
Bayesian Prediction
Want to predict
- Predictions are weighted averages of the predictions of the individual hypotheses
- Hypotheses serve as intermediaries between raw data and prediction
Bayesian Learning Properties
Optimal:
- given prior, no other prediction is correct more often than the Bayesian one
No overfitting: prior/likelihood booth penalise complex hypotheses
Price to pay:
- Bayesian learning may be intractable when hypothesis space is large
- sum over hypotheses space can be intractable
Solution: Approximate Bayesian Learning
Maximum a Posteriori
Idea: make a prediction based on most probable hypothesis:
Contrast with Bayesian learning where all hypotheses are used
MAP Properties
MAP prediction less accurate than full Bayesian since it relies only on one hypothesis
- MAP and Bayesian predictions converge as data increases
- no overfitting
- Finding
may be intractable
* product induces a non-linear optimisation
- can take the log to linearise
Maximum Likelihood (ML)
Idea: Simplify MAP by assuming uniform prior
- i.e.
Make prediction based on
ML Properties
ML prediction less accurate than Bayesian or MAP prediction since it ignores prior and relies on one hypothesis
- but ML, MAP and Bayesian converge as the amount of data increases
- more susceptible to overfitting: no prior
is often easier to find than
Binomial Distribution
Generalise the hypothesis space to a continuous quantity
(one order) (any order)
Priors on Binomials
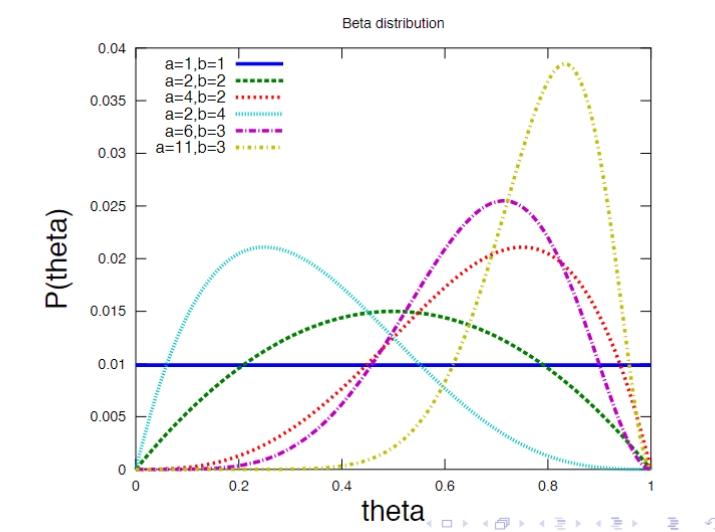
The Beta Distribution
Bayesian Classifiers
Idea: if you knew the classification you could predict the values of features
Naïve Bayesian Classifier
- Requires:
and for each
Predict class
- Parameters:
- Assumption:
s are independent given
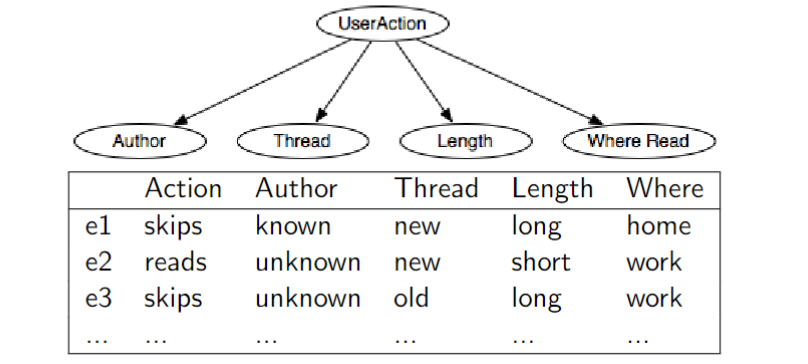
ML sets:
to relative frequency of reads, skips to relative frequency of given reads, skips

Laplace Correction
If a feature never occurs in the training set, but does in the test set
- ML may assign zero probability to a high likelihood class
- add 1 to the numerator, and add
(arity of variable) to the denominator - assign:
- like a pseudocount
Bayesian Network Parameter Learning (ML)
For fully observed data
- Parameters
- CPTS
- Data d:$$d_1 = < V_1=v{1, 1}, V_2 = v_{2, 1},\cdots, V_n=v_{n, 1}>$$$$d_2 = < V_2=v{1, 2}, V_2 = v_{2, 2},\cdots, V_n=v_{n, 2}>$$
Maximum likelihood: Setto the relative frequency of values of given the values v of the parents of
Occam’s Razor
Simplicity is encouraged in the likelihood function:
is more complex (lower bias) than - so can explain more datasets
- but each with lower probability (higher variance)
Supervised Machine Learning
Linear Regression
Linear regression is a model in which the output is a linear function of the input features
where
The sum o squares error on examples
Goal: Find weights that minimize
Finding weights that minimize
Find the minimum analytically
- Effective when it can be done
If is a vector of the output features for the examples is a matrix where the column is the values of the input features for the example is a vector of weights
then
Find the minimum iteratively
- works for larger classes of problem (not just linear)
Gradient Descent
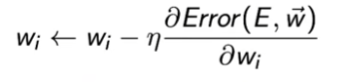
If
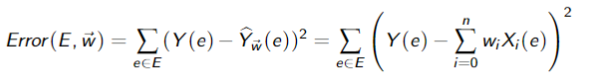
then update rule:
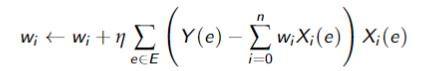
where we have set

Stochastic and Batched Gradient Descent
- If examples are chosen randomly at line 8 then its stochastic gradient descent
- Batched gradient descent:
- process a bath of size
before updating the weights - if
is all the data, then its gradient descent - if
, its incremental gradient descent
- process a bath of size
- Incremental can be more efficient than batch, but convergence not guaranteed
Linear Classifier
Assume we are doing binary classification, with classes
- There is no point in making a prediction of less than 0 or greater than 1
- A squashed linear function is of the form:
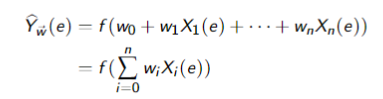
whereis an activation function - A simple activation function is the step function:
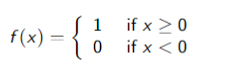
Gradient Descent for Linear Classifiers
If the activation function is differentiable, we can use gradient descent to update the weights. The sum of squares error:
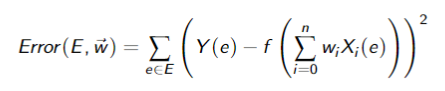
The partial derivative with respect to weight
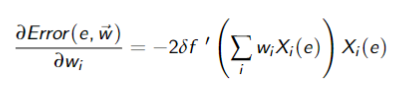
where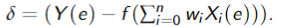
Thus, each example
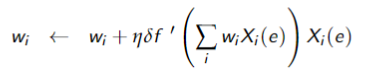
The sigmoid or logistic activation function
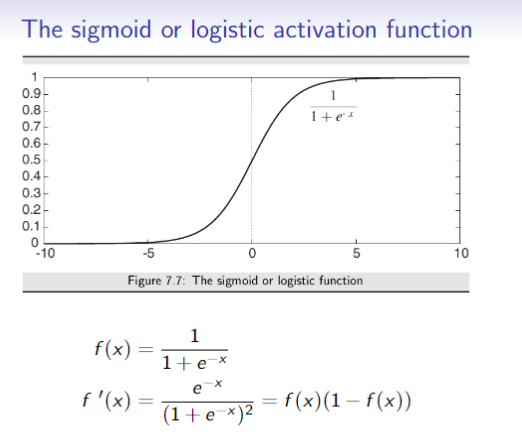
So,
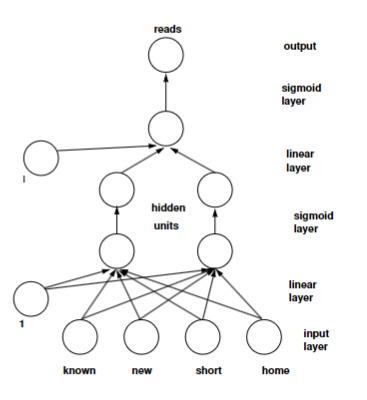
Neural Networks
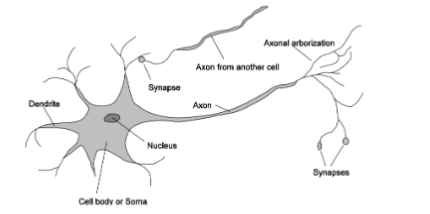
- Inspired by biological networks
- connect up many simple units
- simple neuron: threshold and fire
- can help gain understanding of how biological intelligence works
- can learn the same things that a decision tree can
- imposes different learning bias
- way of making new predictions
- back-propagation learning:
- errors made are propagated backwards to change the weights
- Often the linear and sigmoid layers are treated as a single layer
Neural Networks Basics
- Each node
has a set of weights - Each node
receives inputs - number of weights = number of parents + 1
constant bias term
- output is the activation function output
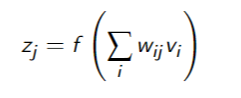
- necessarily non-linear
- because a linear function of a linear function is a… linear function
Activation Functions
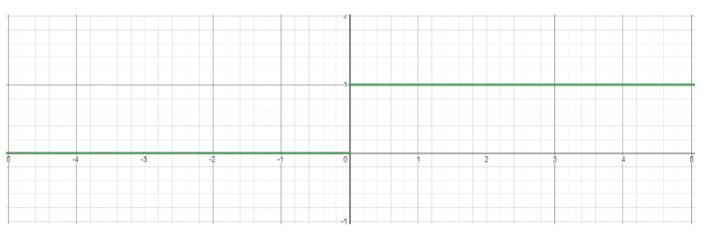
- Step function
- integrate-and-fire (biological)
if else - simple to use, but not differentiable
- Not used in practice
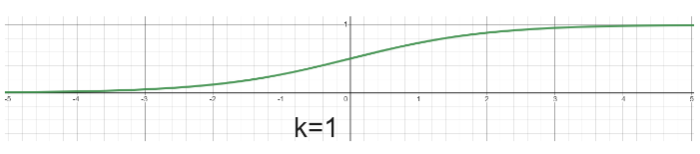
- Sigmoid function
- For very large or very small
, is very close to 1 or 9 - Can approximate the step function by tuning
- As
increases, the sigmoid function becomes steeper and is closer to the step function - Usually in practice
- As
- Differentiable
- Vanishing gradient problem:
- when
is very large or very small, responds little to changes in - the network does not learn further or learns very slow
- when
- Computationally expensive
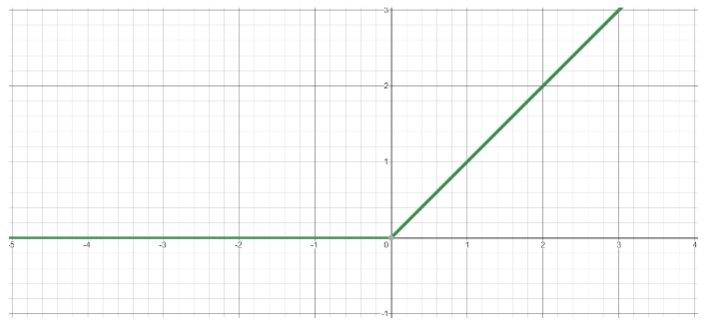
- Rectified Linear Unit (ReLU)
- Computationally efficient
- network converges quickly
- Differentiable
- The dying ReLU problem:
- when inputs approach 0 or are negative, the gradient becomes 0 and the network cannot learn
- when inputs approach 0 or are negative, the gradient becomes 0 and the network cannot learn
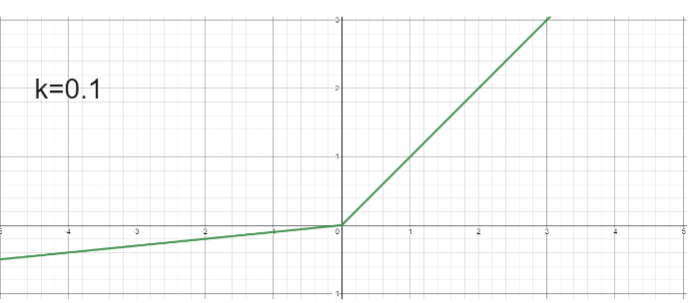
- Leaky ReLU
- Small positive slope
in the negative area - enables learning for negative input values
Connecting the neurons together in to a network
Feedforward Network
- Forms a directed acyclic graph
- Have connections only in one direction
- Represents a function of its inputs
Recurrent Network - Feed its outputs back into its inputs
- Can support short-term memory
- For the given inputs, the behaviour of the networks depends on its initial state
- which may depend on previous inputs
- The model is more interesting, but more difficult to understand and to learn
Learning Weights
Back-propagation implements stochastic gradient descent
- Recall:
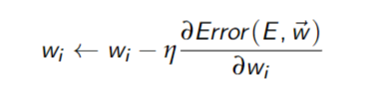
: learning rate
The Backpropagation Algorithm
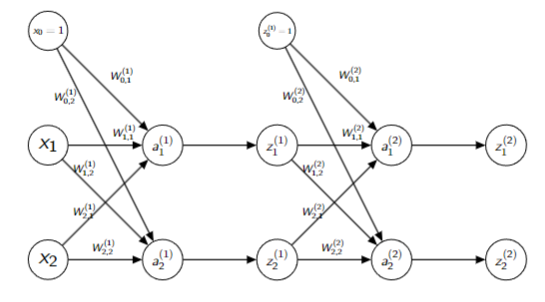
An efficient method of calculating the gradients in a multi-layer neural network
- Given training examples
and an error/loss function . Perform 2 passes - Forward pass:
- compute the error
given the inputs and the weights
- compute the error
- Backward pass:
- compute the gradients
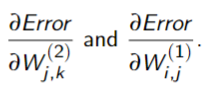
- compute the gradients
- Forward pass:
- Update each weight by the sum of the partial derivatives for all the training examples
Improving Optimization
- Momentum: weight changes accumulate over iterations
- RMS-Prop: rolling averages of square of gradient
- Adam: combination of Momentum and RMS-Prop
- Initialization: randomly set parameters to start
Improving Generalization: Regularization
Regularized Neural nets: prevent overfitting, increased bias for reduced variance
- parameter norm penalties added to objective function
- dataset augmentation
- early stopping
- dropout
- parameter typing
- Convolutional neural nets:
- used for images, parameters tied across space
- Recurrent neural nets:
- used for sequences, parameters tied across time
- Convolutional neural nets:
Sequence Modeling
- Word Embeddings:
- latent vector spaces that represent the meaning of words in context
- RNNs: NN repeats over time and has inputs from previous time step
- LSTM:
- RNN with longer-term memory
- Attention:
- uses expected embeddings to focus updates on relevant parts of the network
- Transformers:
- multiple attention mechanisms
- LLMs:
- very large transformers for language
Composite models and other learning methods
- Random Forests
- Each decision tree in the forest is different
- different features, splitting criteria, training sets
- average or majority vote determines output
- Each decision tree in the forest is different
- Support Vector Machines
- find the classification boundary with the widest margin
- combine with the kernel trick
- Ensemble Learning
- combination of base-level algorithms
- Boosting
- sequence of learners fitting the examples the previous learner did not fit well
- learners progressively biased towards higher precision
- early learners:
- lots of false positives, but reject all the clear negatives
- later learners:
- problem is more difficult, but the set of examples is more focused around the challenging boundary
- sequence of learners fitting the examples the previous learner did not fit well
Unsupervised Machine Learning
Incomplete data
Many real-world problems have hidden variables (AKA latent variables)
- incomplete data
- values of some attributes missing
Incomplete data → unsupervised learning
How to Deal with Missing Data
- Ignore hidden variables
- Complexity increases
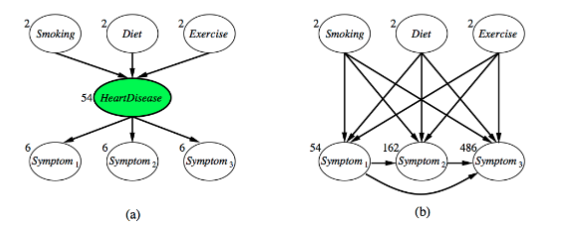
- Complexity increases
- Ignore records with missing values
- does not work with true latent variables
- e.g. always missing
- does not work with true latent variables
Often data is missing because of something correlated with a variable of interest
- For example: data in a clinical trial to test a drug may be missing because:
- the patient dies
- the patient dropped out because of severe side effects
- they dropped out because they were better
- the patient had to visit a sick relative
- ignoring some of these mat make the drug look better or worse than it is
In general, you need to model why data is missing
- maximize likelihood directly
- suppose
is hidden and is observable with values
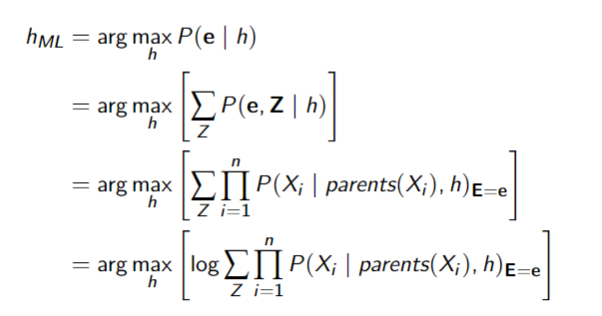
- suppose
Expectation-Maximization (EM)
If we knew the missing values, computing
- Guess
- iterate:
- expectation: based on
, compute expectation of missing values - maximization: based on expected missing values, compute new estimate of
- expectation: based on
Really simple version (K-means algorithm)
Expectation: based on
Maximization: based on those missing values, you now have complete data
- so compute new estimate of
using ML learning as before
K-Means Algorithm
K-means algorithm can be used for clustering:
- dataset of observables with input features
generated by one of a set of classes,
Inputs: - training examples
- the number of classes,
Outputs: - a representative value for each input feature for each class
- an assignment of examples to classes
Algorithms:
- pick
means in , one per class, - iterate until means stop changing:
- assign examples to
classes (e.g. as closest to current means) - re-estimate
-means based on assignment
- assign examples to
Expectation Maximization
Approximate the maximum likelihood
- Start with a guess
- Iteratively compute:
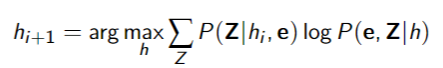
- expectation: compute
- ”fills in” missing data
- maximization: find new
that maximizes
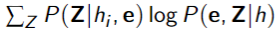
- can show that
when computed like this
General Bayes Network EM
Complete Data: Bayes Net Maximum Likelihood
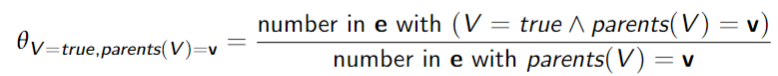
Incomplete data: Bayes Net Expectation Maximization
- observed variables
and missing variables - Start with some guess for
E Step: Compute weights for each dataand latent variable(s) value(s) - using e.g. variable elimination
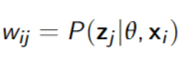
M Step: Update parameters:
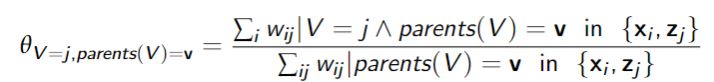
Belief Network Structure Learning

- A model here is a belief network
- A bigger network can always fit the data better
lets us encode a preference for smaller networks - e.g. using the description length
- You can search over network structure looking for the most likely model
Can do independence tests to determine which features should be the parents - XOR problem:
- just because features do not give information individually, does not mean they will not give information in combination
- ideal: Search over total orderings of variables
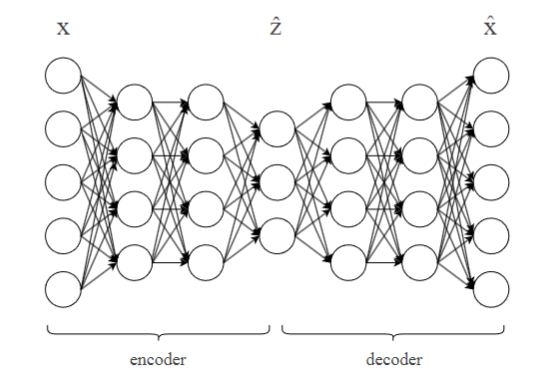
Autoencoders
A representational learning algorithm
- Learn to map examples to low-dimensional representation
Components
2 main components:
- Encoder
: maps to low-dimensional representation - Decoder
: maps to its original representation
Autoencoder implements
is the reconstruction of original input - Encoder and decoder learned such that
contains as much information about as needed to reconstruct it
Minimize sum of squares of differences between input and prediction:
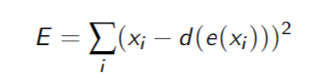
Deep Neural Network Autoencoders
- good for complex inputs
and are feedforward neural networks, joined in series - Train with backpropagation
Generative Adversarial Networks
A generative unsupervised learning algorithm
- Goal is to generate unseen examples that look like training examples
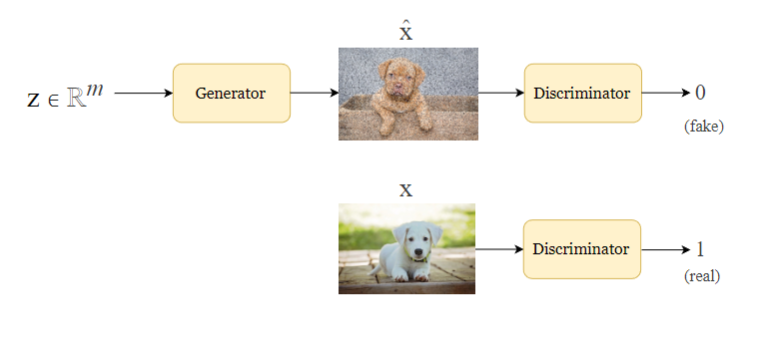
Components
GANs are actually a pair of neural networks:
- Generator
: Given vector in latent space, produces example drawn from a distribution that approximates the true distribution of training examples sampled from a Gaussian distribution
- Discriminator
: A classifier that predicts whether is real (from training set) or fake (made by )
Training
GANs are trained with a minimax error:
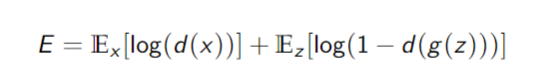
- Discriminator tries to maximize
- for
from the training set, - for
from the generator,
- for
- Generator tries to minimize
- tries to fool - for
from the training set, - for
from the generator,
After convergence:
- for
should be producing realistic images should output , indicating maximal uncertainty
