Inference and Planning
Problem Solving
Two methods for solving problems
- Procedural:
- Devise an algorithm
- Program the algorithm
- Execute the program
- Declarative:
- Identify the knowledge needed
- Encode the knowledge in a representation
- Knowledge Base (KB)
- Use logical consequences of KB to solve the problem
Proof Procedures
A logic consists of
- Syntax: what is an acceptable sentence?
- Semantics: what do the sentences and symbols mean?
- Proof procedure: how do we construct valid proofs?
A proof: a sequence of sentences derivable using an inference rule
Common Rules
De Morgan’s Laws
Modus Ponens
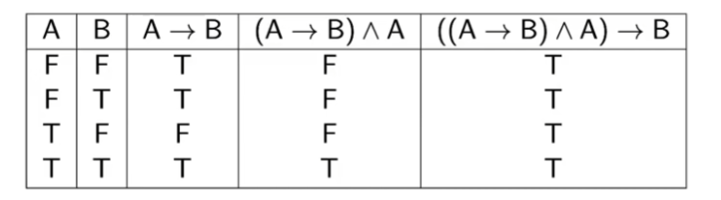
Modus Ponens is a Tautology
- Always true!
- If it’s raining then the grass is wet
- It’s raining
- Therefore the grass is wet
Modus Tolens
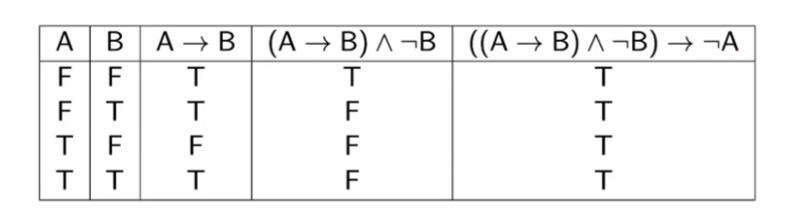
Modus Tolens is a Tautology
- Always true!
- If it’s raining then the grass is wet
- The grass is not wet
- Therefore it is not raining
Logical Consequence
is a set of statements - A set of truth assignments to
is an interpretation - A model of
is an interpretation that makes true - We say that the world in which these truth assignments hold is a model of
- A verifiable example
is inconsistent if it has no model
If, for every set of truth assignments that hold for
- Then this other statement is a logical consequence of
Argument Validity
An argument is valid if any of the following is true:
- the conclusions are a logical consequence of the premises
- the conclusions are true in every model of the premises
- there is no situation in which the premises are all true, but the conclusions are false
- argument → conclusions is a tautology
(these four statement are identical)
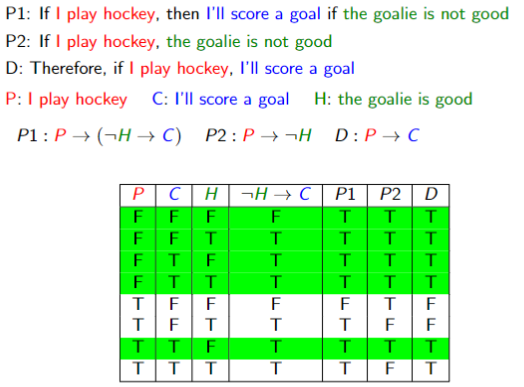
Every row is an interpretation:
- An assignment of T/F to each proposition
Whenever
is a logical consequence:
- If there is no model of the premises, the argument is valid
Deduction and Proof
Given a knowledge base, we want to prove things that are true
- We can use
- Truth Tables
- Natural Deduction
- Semantic Tableaux
- Axiomatic Logic
- Resolution Refutation
Proofs
- A Knowledge Base (KB) is a set of axioms
- A proof procedure is a way of Proving Theorems
means can be derived from using the proof procedure - If
, then is a theorem - A proof procedure is sound:
- if
then
- if
- A proof procedure is complete:
- if
then
- if
- Two types of proof procedures
- Bottom up and top down
Complete Knowledge
We assume a closed world
- the agent knows everything
- can prove everything
- if it can't prove something:
- must be false
- negation as failure
Other option is an open world:
- the agent doesn’t know everything
- can’t conclude anything from a lack of knowledge
Bottom-Up Proof
AKA forward chaining
- Start from facts and use rules to generate all possible atoms

Sound and Complete
Top-Down Proof
Start from query and work backwards

Beyond Propositions: Individuals and Relations
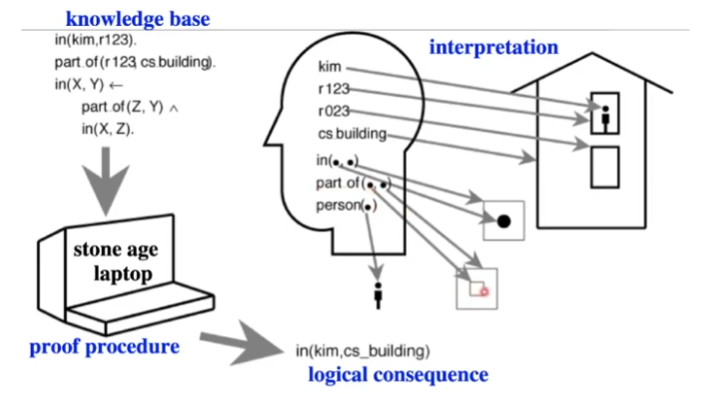
- KB can contain relations:
part_of(C, A)is true if C is a “part of” A (in the real world)
- KB can contain quantification:
part_of(C, A)holds
- proof procedure is the same, with a few extra bits to handle relations & quantification
Planning
Planning is deciding what to do based on an agent’s ability, its goal, and the state of the world
- Planning is finding a sequence of actions to solve a goal
Initial assumptions: - A single agent
- The world is deterministic
- There are no exogenous events outside of the control of the agent that change the state of the world
- The agent knows what state it is in
- full observability
- Time progresses discretely from one state to the next
- Goals are predicates of states that need to be achieved or maintained
- No complex goals
Actions
- A deterministic action is a partial function from states to states
- Partial function:
- Some actions not possible in some states
- The preconditions of an action specify when the action can be carried out
- The effect of an action specifies the resulting state
Example
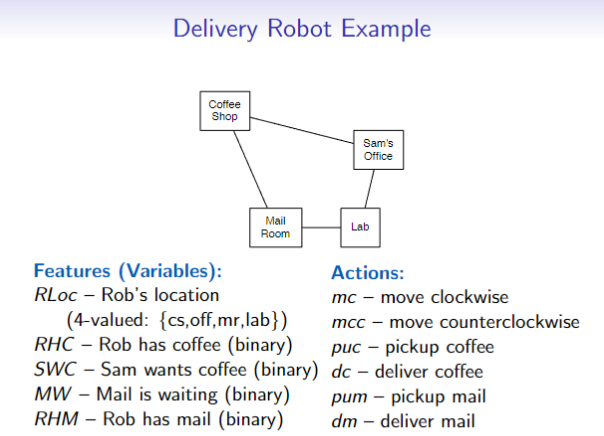
Explicit State-Space Representation
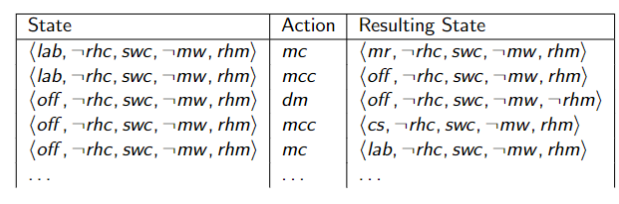
Feature-Based Representation of Actions

For each action:
- precondition is a proposition that specifies when the action can be carried out
For each feature: - casual rules that specify when the feature gets a new value and
- frame rules that specify when the feature keeps its value
Notation: - Features are capitalized (e.g. Rloc, RHC)
- Values of the features are not (e.g. Rloc = cs, rhc,
rhc) - If
is a feature, then is the feature after an action is carried out
Planning
Given:
- A description of the effects and preconditions of the actions
- A description of the initial state
- A goal to achieve
Find a sequence of actions that is possible and will result in a state satisfying the goal
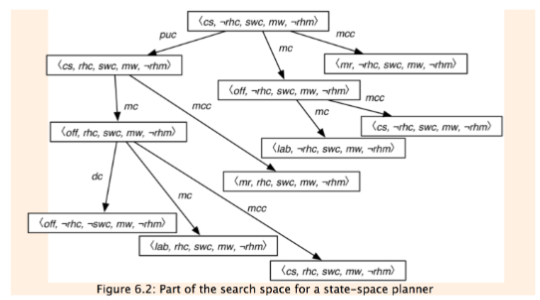
Forward Planning
Idea: search in the state-space graph
- The nodes represent the states
- The arcs correspond to the actions:
- The arcs from a state
represent all of the actions that are legal in state
- The arcs from a state
- A plan is a path from the state representing the initial state to a state that satisfies the goal
- Heuristics important
Example state-space graph
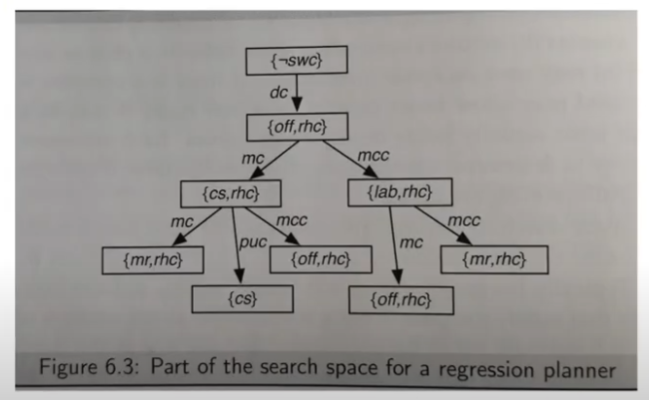
Regression Planning
Idea: search backwards from the goal description
- Nodes corresponds to subgoals, and arcs to actions
- Nodes are propositions:
- a formula made up of assignments of values to features
- Arcs correspond to actions that can achieve one of the goals
- Neighbors of a node
associated with arc specify what must be true immediately before so that is true immediately after - The start node is the goal to be achieved
is true if is a proposition that is true of the initial state
Example