Features and Constraints

Constraint Satisfaction Problems (CSPs)

• A set of variables
• a domain for each variable
• A set of constraints or evaluation functions
• Two kinds of problems:
  1. Satisfiability Problems:
     • Find an assignment that satisfies constraints (hard constraints)
  2. Optimization Problems:
     • Find an assignment that optimises the evaluation function (soft constraints)
• A solution to a CSP is an assignment to the variables that satisfies all constraints
• A solution is a model of the constraints

CSPs as Graph Searching Problems

Two ways to represent CSPs as a graph searching:

• Complete Assignment:
  • Nodes:
    • assignment of value to all variables
  • Neighbors:
    • change one variable value
• Partial assignment:
  • Nodes:
    • assignment to first $k-1$ variables
  • Neighbors:
    • assignment to $k^{th}$ variable
      But,
• These search spaces can get extremely large (thousands of variables), so the branching factors can be big
• Path to goal is not important, only the goal is
• No predefined starting nodes

Classic CSP: Crossword Construction

Dual Representations

Two ways to represent the crossword as a CSP

• Primal representation
  • Nodes represent word positions: 1-down, …, 6-across
  • Domains are the words
  • Constraints specify that the letters on the intersections must be the same
• Dual representation
  • Nodes represent the individual squares
  • Domains are the letters
  • Constraints specify that the words must fit

Posing a CSP

Variables: $V_1,V_2,\cdots ,V_n$
Domains: for each variable, $V_i$ has a domain $D_{v_i}$
Constraints: Restrictions on the values a set of variables can jointly have

Constraints

• Can be N-ary, Over sets of $N$ variables
  • e.g. “dual representation” for crossword puzzles with letters as domains
    • word length $n$ with constraint for each letter
    • $n$ variables
• Here: Consider only Unary and Binary
  • e.g. “first representation” for crossword puzzles with words as domains
    • constraint on word length and intersection
    • 1 or 2 variables

Solutions:

Generate and test

• Generate all possible assignments and test if it satisfies

Backtracking

• able to prune branches
• evaluate constraints as soon as they are grounded
• traverse in order

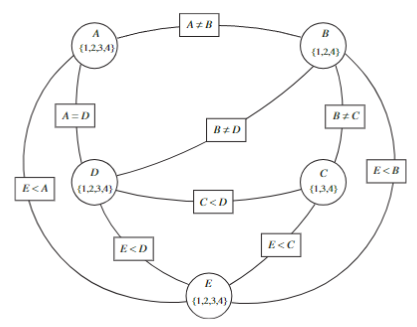
Consistency

• More general approach
• look for inconsistencies
  • e.g. C=4 is inconsistent with any value of D since $C<D$
  • backtracking will “re-discover” this for every value of A, B
• graphical representation of constraints
  
• Constraint Network (CN)
• domain constraint is unary constraint on values in a domain, written as $(X,c(X))$
• A node in a CN is domain consistent if no domain value violates any domain constraint
• A CN is domain consistent if all nodes are domain consistent
• Arc $(X,x(X,Y))$ is a constraint on $X$
• An arc $(X,x(X,Y))$ is arc consistent if for each $X\in D_X$, there is some $Y\in D_Y$ such that $c(X,Y)$ is satisfied
  • Bi-directional
• A CN is arc consistent if all arcs are arc consistent
• A set of variables $\{X_1,X_2,X_3,\cdots ,X_N\}$ is path consistent if all arcs and domains are consistent
  Formal Representation:
  

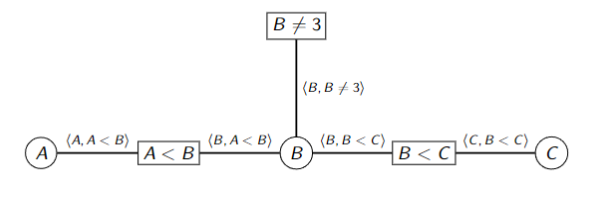
AC-3

Makes a CN arc consistent and domain consistent

• To-Do Arcs Queue (TDA) has all inconsistent arcs

When AC-3 Terminates

AC-3 always terminates with one of these three conditions:

• Every domain is empty:
  • there is no solution
• Every domain has a single value:
  • has solution!
• Some domain has more than one value:
  • split it in two, run AC-3 recursively on two halves
  • don’t have to start from scratch
    • only have to put back all arcs $(Z,c^{\prime }(Z,X))$ if $X$ was the domain that was split
  • Connection between domain splitting and search

Complexity

• $n$ variables, $c$ binary constraints, and the size of each domain is at most $d$
• Time complexity: $O(c{d}^3)$
  • Each arc $(X_k,X_i)$ can be added to the queue at most $d$ times because we can delete at most $d$ values from $X_i$
• Checking consistency of each arc can be done in $O(d^2)$ time

Variable Elimination

Idea: Eliminate the variables one-by-one passing their constraints to their neighbors

• When there is a single variable remaining, if it has no values, the network was inconsistent
• The variables are eliminated according to some elimination ordering
• Different elimination orderings result in different size intermediate constraints

Hill-Climbing

Randomized incl. Local Search

Local Search

• Maintain an assignment of a value to each variable
• At each step, select a neighbor of the current assignment
  • e.g. one that improves some heuristic value
• Stop when a satisfying assignment is found, or return the best assignment found

Requires:

• What is a neighbor?
• Which neighbor should be selected?

Local Search for CSPs

• Aim is to find an assignment with zero unsatisfied constraints
• Given an assignment of a value to each variable, a conflict is an unsatisfied constraint
• The goal is an assignment with zero conflicts
• Heuristic function to be minimized:
  • the number of conflicts

Greedy Descent Variants

• Find the variable-pair that minimizes the number of conflicts at every step
• Select a variable that participates in the most number of conflicts. Select a value that minimizes the number of conflicts
• Select a variable that appears in any conflict. Select a value that minimizes the number of conflicts
• Select a variable at random. Select a value that minimizes the number of conflicts
• Select a variable and value at random; accept this change if it doesn’t increase the number of conflicts

Problems with Greedy Descent

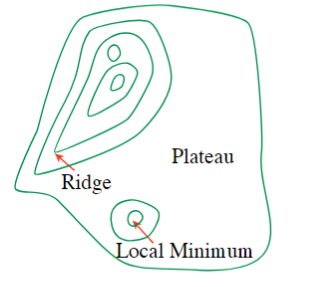
• A local minimum that is not a global minimum
• A plateau where the heuristic values are uninformative
• A ridge is a local minimum where $n$-step look ahead might help

Randomized Greedy Descent

As well as downward steps we can allow for:

• Random steps: move to a random neighbor
• Random restart: reassign random values to all variables
  Which is more expensive computationally?
• A mix of the two = stochastic local search

High Dimensional Search Spaces

• In high dimensions the search space is less easy to visualize
• Often consists of long, nearly flat ”canyons”
• Hard to optimize using local search
• Step-size can be adjusted

Stochastic Local Search

A mix of:

• Greedy descent:
  • Move to a lowest neighbor
• Random walk:
  • Taking some random steps
• Random restart:
  • Reassigning values to all variables

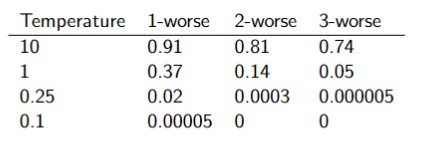
Variant: Simulated Annealing

• Pick a variable at random and a new value at random
• If it is an improvement, adopt it
• If it isn’t an improvement, adopt it probabilistically depending on a temperature parameter, $T$
  • With current assignment $n$ and proposed assignment $n^{\prime }$ we move to $n^{\prime }$ with probability $e^{(-h(n^{\prime })-h(n))/T}$
• Temperature can be reduced
  Probability of accepting a change:
  

Tabu Lists

• recall GSAT:
  • never choose same variable twice
• To prevent cycling we can maintain a tabu list of the $k$ last assignments
• Don’t allow an assignment that is already on the tabu list
• If $k=1$, we don’t allow an assignment of to the same value to the variable chosen
• We can implement it more efficiently than as a list of complete assignments
• It can be expensive if $k$ is large

Parallel Search

A total assignment is called an individual

• Maintain a population of $k$ individuals instead of one
• At every stage, update each individual in the population
• Whenever an individual is a solution, it can be reported
• Like $k$ restarts, but uses $k$ times the minimum number of steps

Beam Search

• Like parallel search, with $k$ individuals, but choose the $k$ best out of all of the neighbors
  • all if there are less than $k$
• When $k=1$, it is greedy descent
• The value of $k$ lets us limit space and parallelism

Stochastic Beam Search

Like beam search, but it probabilistically chooses the $k$ individuals at the next generation

• The probability that a neighbor is chosen is proportional to its heuristic value:
  • $e^{-h(n)/T}$
• This maintains diversity amongst the individuals
• The heuristic value reflects the fitness of the individual
• Like asexual reproduction:
  • each individual mutates and the fittest ones survive

Genetic Algorithms

Like stochastic beam search, but pairs of individuals are combined to create the offspring:

• For each generation:
  • Randomly choose pairs of individuals where the fittest individuals are more likely to be chosen
  • For each pair, perform a cross-over: form two offspring each taking different parts of their parents:
    • Mutate some values
• Stop when a solution is found

Crossover

• Given two individuals:

• Select $i$ at random
• Form two offspring:

• The effectiveness depends on the ordering of the variables
• Many variations

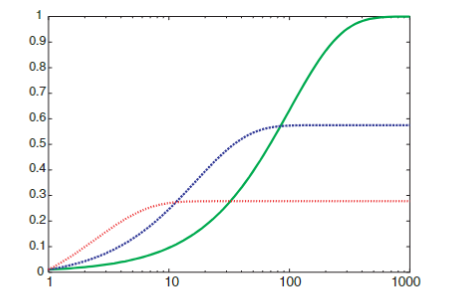
Compare Stochastic Algorithms

How can you compare three algorithms when

• One solves the problem 30% of the time very quickly but doesn’t halt for the other 70%
• One solves 60% of the cases reasonably quickly but doesn’t solve the rest
• One solves the problem in 100% of the cases, but slowly