Decision Making

Planning Under Uncertainty

Bayesian Decision Making

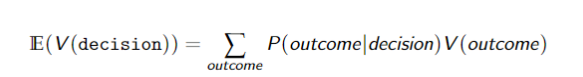
Can also add context so $V(decision,context)$ is the value of decision in situation context

Preferences

• Actions result in outcomes
• Agents have preferences over outcomes
• A (decision-theoretic) rational agent will do the action that has the best outcome for them
  • Sometimes agents don’t know the outcomes of the actions, but they still need to compare actions
  • Agents have to act
    • doing nothing is often a meaningful action

Preferences Over Outcomes

If $o_1$ and $o_2$ are outcomes

• $o_1⪰o_2$ means $o_1$ is at least as desirable as $o_2$
  • weak preference
• $o_1\sim o_2$ means $o_1⪰o_2$ and $o_2⪰o_1$
  • indifference
• $o_1\succ o_2$ means $o_1⪰o_2$ and $o_2⋡o_1$
  • strong preference

Lotteries

An agent may not know the outcomes of their actions, but only have a probability distribution of the outcomes

• A lottery is a probability distribution over outcomes. It is written $$\left[p_1:o_1, p_2:o_2, \cdots, p_k:o_k\right]$$where the $o_i$ are outcomes and $p_i>0$ such that$$\sum_ip_i = 1$$The lottery specifies: outcome $o_i$ occurs with probability $p_i$
  When we talk about outcomes, we will include lotteries

Properties of Preferences

Completeness

• Agents have to act, so they must have preferences
  
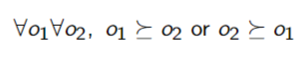
  Transitivity
• Preferences must be transitive
  
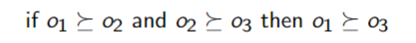
  Monotonicity
• An agent prefers a larger chance of getting a better outcome than a smaller chance
  
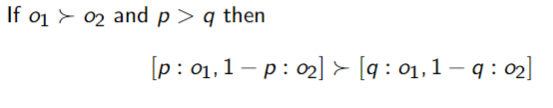
  Continuity
• Suppose $o_1\succ o_2$ and $o_2\succ o_3$, then there exists a $p\in [0,1]$ such that
  
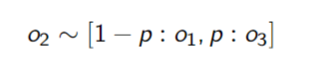
  Decomposability
• An agent is indifferent between lotteries that have same probabilities and outcomes
  Substitutability
• if $o_1\sim o_2$ then the agent is indifferent between lotteries that only differ by $o_1$ and $o_2$

Theorem

If preferences follow the preceding properties, then the preferences can be measured by a function

such that

• $o_1⪰o_2$ if and only if $utility(o_1)\ge utility(o_2)$
• Utilities are linear with probabilities:
  

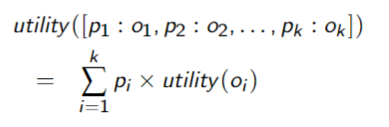
Rationality and Irrationality

Rational agents act so as to maximize expected utility:

• Action $a_1$ leads to outcome $[o_1,\cdots ,o_l]$ with probabilities $[p_1,\cdots ,p_k]$
• Action $a_2$ leads to outcome $[o_1,\cdots ,o_l]$ with probabilities $[q_1,\cdots ,q_k]$
• if $\sum _{i=1}^k{p}_i\times utility(o_i)>\sum _{i=1}^k{q}_i\times utility(o_i)$
  • then action $a_1$ is the rational choice

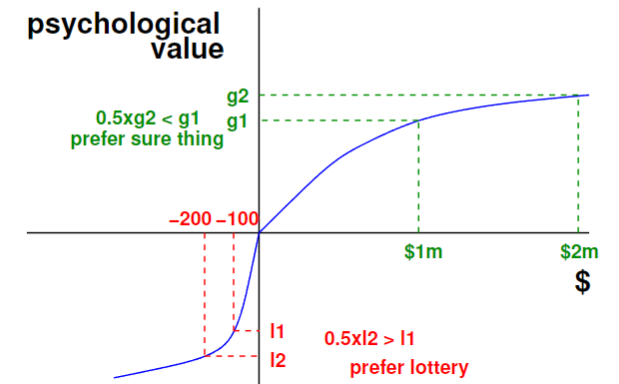
Prospect Theory - Tversky and Kahneman

Humans weight value differently for gains vs losses

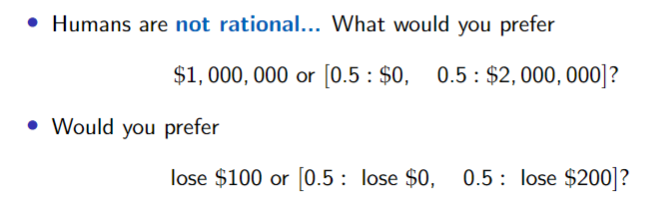
Ultimatum Game

• Two-player game: agents $A$ and $B$
• $A$ gets $10
• $A$ can offer $B$ any amount $x=\mathrm{\$}[0-10]$
• $B$ can
  • accept: $B$ gets $x$, $A$ gets $10-x$
  • reject: $A$ and $B$ both get 0
• rational choice: $A$ offers $B$ $ϵ\to 0$, $B$ accepts
• Humans: $x\approx \mathrm{\$}4$

Making Decisions Under Uncertainty

What an agent should do depends on:

• The agent’s ability
  • what options are available to it
• The agent’s beliefs
  • the ways the world could be, given the agent’s knowledge
  • Sensing the world updates the agent’s beliefs
• The agent’s preferences
  • what the agent actually wants and the tradeoffs when there are risks
    Decision theory specifies how to trade off the desirability and probabilities of the possible outcomes for competing actions

Single Decisions

Decision variables are like random variables that an agent gets to choose the value of

• Ina single decision variable, the agents can choose $D=d_i$ for any $f_i\in dom(D)$
  Expected utility of decision $D=d_i$ leading to outcomes $\omega$ for utility function $u$
  
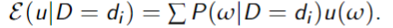
  An optimal single decision is the decision $D=d_{max}$ whose expected utility is maximal:
  

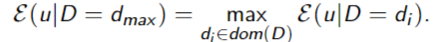
Decision Networks

A decision network is a graphical representation of a finite sequential decision problem

• Decision networks extend belief networks to include decision variables and utility
  A decision network specifies what information is available when the agent has to act
  A decision network specifies which variables the utility depends on
  
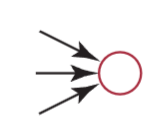
  A random variable is drawn as a ellipse
• Arcs into the node represent probabilistic dependence
  
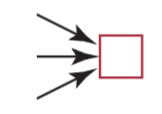
  A decision variable is drawn as a rectangle
• Arcs into the node represent information available when the decision is made
  
  A utility node is drawn as a diamond
• Arcs into the node represent variables that the utility depends on

Example

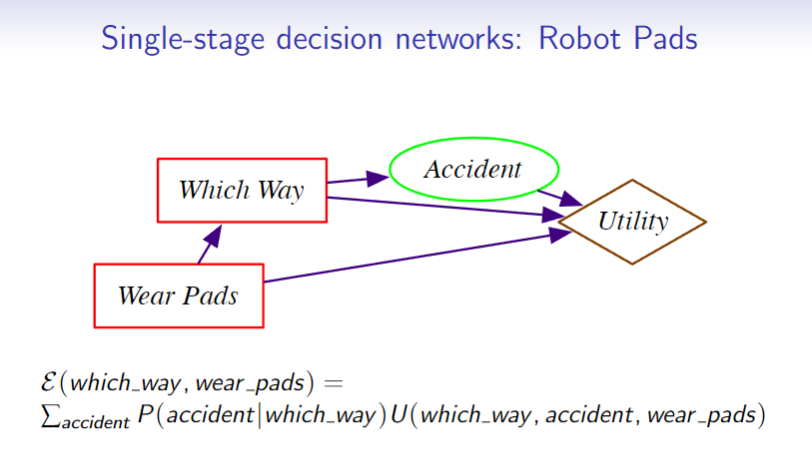
Finding the Optimal Decision

Suppose the random variables are $X_1,\cdots ,X_n$, decision variables are $D$, and utility depends on $X_{i1},\cdots ,X_{ik}$ and $D$:

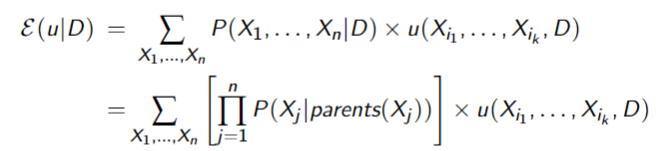
• where $parents(X_j)$ may include $D$
  To find the optimal decision:
• Create a factor for each conditional probability and for the utility
• Multiply together and sum out all of the random variables
• This creates a factor on $D$ that gives the expected utility for each $D$
• Choose the $D$ with the maximum value in the factor

Sequential Decisions

An intelligent agent doesn’t make a multi-step decision and carry it out without considering revising it based on future information

• A more typical scenario is where the agent:
  • observes, acts, observes, acts
• Subsequent actions can depend on what is observed
  • What is observed depends on previous actions
• Often the sole reason for carrying out an action is to provide information for future actions
  • e.g. diagnostic tests, spying

Sequential decision problems

A sequential decision problem consists of a sequence of decision variables $D_1,\cdots ,D_n$

• Each $D_i$ has an information set of variables $parents(D_i)$, whose value will be known at the time decision $D_i$ is made

Policies

A policy specifies what an agent should do under each circumstance

• A policy is a sequence ${\delta }_1,\cdots ,{\delta }_n$ of decision functions$$\delta_i : dom(parents(D_i)) \rightarrow dom(D_i)$$
  This policy means that when the agent has observed $O\in dom(parents(D_i))$, it will do ${\delta }_i(O)$

Expected Utility of a Policy

The expected utility of policy $\delta$ is

An optimal policy is one with the highest expect utility

Finding the Optimal Policy

1. Create a factor for each conditional probability table and a factor for the utility
2. Set remaining decision nodes ← all decision nodes
3. Multiply factors and sum out variables that are not parents of a remaining decision node
4. Select and remove a decision variable $D$ from the list of remaining decision nodes:
   1. pick one that is in a factor with only itself and some of its parents (no children)
5. Eliminate $D$ by maximizing. This returns:
   1. the optimal decision function for $D$, $argma{x}_{D}f$
   2. a new factor to use, $\underset{D}{max}f$
6. Repeat 3-5 until there are no more remaining decision nodes
7. Eliminate the remaining random variables
   1. Multiply the factors: this is the expected utility of the optimal policy
8. If any nodes were in evidence, divide by the P(evidence)

Agents as Processes

Agent carry out actions:

• forever - infinite horizon
• until some stopping criteria is met - indefinite horizon
• finite and fixed number of steps - finite horizon

Decision-Theoretic Planning

What should an agent do when

• it gets rewards and punishments and tries to maximize its rewards received
• actions can be noisy;
  • the outcome of an action can’t be fully predicted
• there is a model that specifies the probabilistic outcome of actions
• the world is fully observable:
  • the current state is always full in evidence

World State

The world state is the information such that if you knew the world state, no information about the past is relevant to the future

• Markovian assumption
  Let $S_i,A_i$ be the state, action at time $i$
  
• $P(s^{\prime }|s,a)$ is the probability that the agent will be in state $s^{\prime }$ immediately after doing action $a$ in state $s$
• The dynamics is stationary if the distribution is the same for each time point

Decision Processes

A Markov decision process augments a Markov chain with actions and values

Markov Decision Processes

For an MDP you specify:

• set $S$ of states
• set of $A$ of actions
• $P(S_t,A_t,S_{t+1})$ specifies the dynamics
• $R(S_t,A_t,S_{t+1})$ specifies the reward.
  • The agents gets a reward at each time step (rather than just a final reward)
  • $R(s,a,s^{\prime })$ is the expected reward received when the agent is in state $s$, does action $a$ and ends up in state $s^{\prime }$

Information Availability

What information is available when the agent decides what to do?

• fully-observable MDP
  • the agent gets to observe $S_t$ when deciding on action $A_t$
• partially-observable MDP (POMDP)
  • the agent has some noisy sensor of the state
  • it needs to remember its sensing and acting history
  • it can do this by maintaining a sufficiently complex belief state

Rewards and Values

Suppose the agent receives the sequence of rewards $r_1,r_2,r_3,r_4,\cdots$ What value should be assigned?

• Total reward $V=\sum _{i=1}^{\mathrm{\infty }}{r}_i$
• Average reward $V=\underset{n\to \mathrm{\infty }}{lim}(r_1+\cdots +r_n)/n$
• Discounted reward $V=r_1+\gamma r_2+{\gamma }^2{r}_3+{\gamma }^3{r}_4+\cdots$
  • $\gamma$ is the discount factor $0\le \gamma \le 1$

Policies

A stationary policy is a function:

Given a state $s,\pi (s)$ specifies what action the agent who is following $\pi$ will do

• An optimal policy is one with maximum expected discounted reward
• For a fully-observable MDP with stationary dynamics and rewards with infinite or indefinite horizon, there is always an optimal stationary policy

Value of a Policy

• $Q^{\pi }(s,a)$, where $a$ is an action and $s$ is a state, is the expected value of doing $a$ in state $s$, then following policy $\pi$
• $V^{\pi }(s)$, where $s$ is a state, is the expected value of following policy $\pi$ in state $s$
• $Q^{\pi }$ and $S^{\pi }$ can be defined mutually recursively:
  

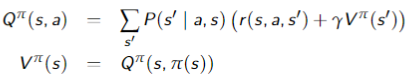
Value of the Optimal Policy

• ${\pi }^{\ast }(s)$ is the optimal action to take in state $s$
• $Q^{\ast }(s,a)$, where $a$ is an action and $s$ is a state, is the expected value of doing $a$ in state $s$, then following the optimal policy ${\pi }^{\ast }$
• $V^{\ast }(s)$, where $s$ is a state, is the expected value of following the optimal policy ${\pi }^{\ast }$ in state $s$
• $Q^{\ast }$ and $S^{\ast }$ can be defined mutually recursively:
  

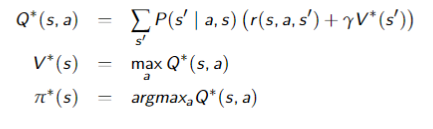
Value Iteration

The $t$-step lookahead value function, $V^t$ is the expected value with $t$ steps to go

• Idea: Given an estimate of the $t$-step lookahead value function, determine the $t+1$-step lookahead value function

Algorithm

• Set $V^0$ arbitrarily, $t=1$
• Compute $Q^t,V^t$ from $V^{t-1}
  
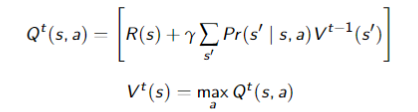
• The policy with $t$ stages to go is simply the action that maximizes this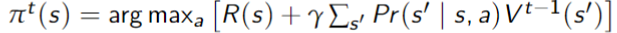
• This is dynamic programming
• This converges exponentially fast (in $t$) to the optimal value function
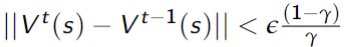
• Convergence when ensures $V^t$ is within $ϵ$ of optimal

Asynchronous Value Iteration

You don’t need to sweep through all the states

• can update the value functions for each state individually
• This converges to the optimal value functions, if each state and action is visited infinitely often in the limit
• You can either store $V[s]$ or $Q[s,a]$

Storing $V[s]$

Repeat forever:

• Select state $s$;
  
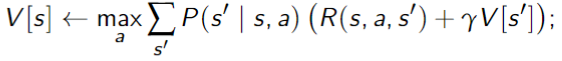
• select action $a$;
  • using an exploration policy

Storing $Q[s,a]$

Repeat forever:

• Select state $s$, action $a$;
  

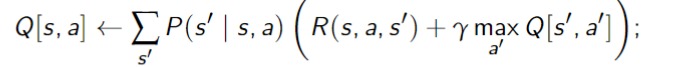
Markov Decision Processes: Factored State

Represent $S=\{X_1,X_2,\cdots ,X_n\}$

• for each $X_i$ and each action $a\in A$, we have $P(X_i^{\prime }|S,A)$
• Reward $R(X_1,X_2,\cdots ,X_n)$ may be additive:

Value iteration proceeds as usual but can do one variable at a time

• e.g. variable elimination

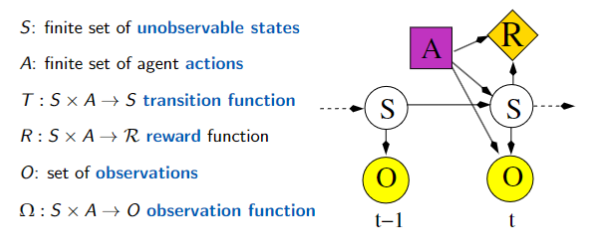
Partially Observable Markov Decision Processes (POMDPs)

A POMDP is like an MDP, but some variables are not observed

• It is a tuple $<S,A,T,R,O,\mathrm{\Omega }>$
  

Value Functions and Conditional Plans

$V(b)$ can be represented with a piecewise linear function over the belief space

• Pieces are called $\alpha$ vectors
  

Monte Carlo Tree Search (MCTS)

Reinforcement Learning

What should an agent do given:

• prior knowledge
  • possible states of the world
  • possible actions
• observations
  • current state of world
  • immediate reward / punishment
• goal
  • act to maximize accumulated reward
    Like decision-theoretic planning, except model of dynamics and model of reward not given
• Need to balance between gathering information and acting optimally

Experiences

We assume there is a sequence of experiences:

• $state,action,reward,state,action,reward,\cdots$
  What should the agent do next?
• It must decide whether to:
  • explore to gain more knowledge
  • exploit the knowledge it has already discovered

Why is reinforcement learning hard?

Credit Assignment Problem: What actions are responsible for the reward may have occurred a long time before the reward was received

• The long-term effect of an action of the robot depends on what it will do in the future
• The explore-exploit dilemma:
  • at each time should the robot be greedy or inquisitive

Main Approaches

See through a space of policies (controllers)

• Model Based RL: Learn a model consisting of state transition function $P(s^{\prime }|a,s)$ and reward function $R(s,a,s^{\prime })$;
  • Solve as an MDP
• Model-Free RL: Learn $Q^{\ast }(s,a)$, use this to guide action.

Temporal Differences

Suppose we have a sequence of values: $$v_1, v_2, v_3, \cdots$$ And want a running estimate of the average of the first $k$ values: $$A_k = \frac{v_1+\cdots + v_k}{k}$$
When a new value $v_k$ arrives:

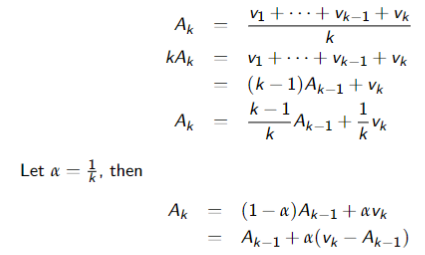
”TD formula”

• Often we use this update with $\alpha$ fixed

Q-Learning

Idea: store $Q[State,Action]$

• Update this as in asynchronous value iteration
• but using experience (empirical probabilities and rewards)
  Suppose the agent has an experience $<s,a,r,s^{\prime }>$
• This provides one piece of data to update $Q[s,a]$
• The experience $<s,a,r,s^{\prime }>$ provides the data point:$$r + \gamma \max_{a'}Q[s',a']$$which can be used in the TD formula giving:
  

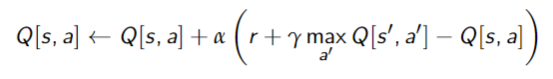
Pseudocode

Properties of Q-learning

Q-learning converges to the optimal policy, no matter what the agent does, as long as it tries each action in each state enough

• But what should the agent do?
  • exploit: when in state $s$, select the action that maximizes $Q[s,a]$
  • explore: select another action

Exploration strategies:

The $ϵ$-greedy strategy:

• choose a random action with probability $ϵ$ and choose a best action with probability $1-ϵ$
  Softmax action selection:
• in state $s$ choose action $a$ with probability
  
• where $\mathrm{\tau }>0$ is the temperature
  • good actions are chosen more often than bad actions
  • $\mathrm{\tau }$ defines how good actions are chosen
  • For $\mathrm{\tau }\to \mathrm{\infty }$, all actions are equiprobable
  • For $\mathrm{\tau }\to 0$, only the best is chosen
    Optimism in the face of uncertainty:
• initialize $Q$ to values that encourage exploration
  Upper Confidence Bound (UCB)
• also store $N[s,a]$
  • number of times that state-action pair has been tried
• and use
  

Model-Based Reinforcement Learning

Model-based reinforcement learning uses the experiences in a more effective manner

• it is used when collecting experiences is expensive
  • e.g. in a robot or an online game
  • and you can do lots of computation between each experience
• idea: learn the MDO and interleave acting and planning
  • After each experience update probabilities and reward
  • then do some steps of asynchronous value iteration

Model-based learner

Off/On-policy Learning

Q-learning does off-policy learning:

• it learns the value of the optimal policy, no matter what it does
• this could be bad if the exploration policy is dangerous
  On-policy learning learns the value of the policy being followed
• e.g. act greedily 80% of the time and act randomly 20% of the time
• If the agent is actually going to explore, it may be better to optimize the actual policy it is going to do
  SARSA uses the experience $<s,a,r,s^{\prime },a^{\prime }>$ to update $Q[s,a]$

SARSA

Q-function Approximations

Let $s=(x_1,x_2,\cdots ,x_N{)}^T$

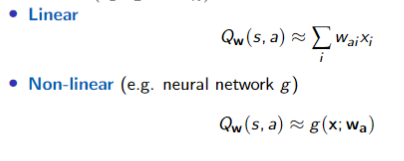
Approximating the Q-function

SARSA with linear function approximation

Convergence

Linear Q-learning $(Q_w(s,a)\approx \sum _i{w}_{ai}{x}_i)$ converges under same conditions as Q-learning

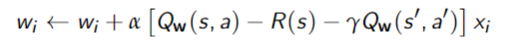
Non-linear Q-learning $(Q_w(s,a)\approx g(x;w))$ may diverge

• Adjusting $w$ to increase $Q$ at $(s,a)$ might introduce errors at nearby state-action pairs

Mitigating Divergence

Two tricks used in practice:

1. Experience Replay
2. Use two $Q$ function (two networks):
   1. $Q$ network (currently being updated)
   2. Target network (occasionally updated)

Experience Replay

Idea: Store previous experiences $(s,a,r,s^{\prime },a^{\prime })$ in a buffer and sample a mini-batch of previous experiences at each step to learn by $Q$-learning

• Breaks correlations between successive updates
  • more stable learning
• Few interactions with environment needed to converge
  • greater data efficiency

Target Network

Idea: use a separate target network that is updated only periodically

• target network has weights $\overline{w}$ and computes $Q_{\overline{w}}(s,a)$
• repeat for each $(s,a,r,s^{\prime },a^{\prime })$ in mini-batch:
  
• $\overline{w}\leftarrow w$

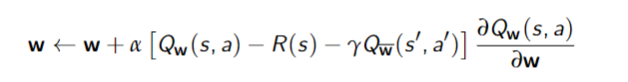
Deep Q-Network

Bayesian Reinforcement Learning

• Include the parameters in the state space
  • transition function and observation function
• Model-based learning through inference
  • belief state
• State space is now continuous
  • belief space is a space of continuous functions
• Can mitigate complexity by modelling reachable beliefs
• optimal exploration-exploitation trade-off