Convolution Layers

Preserve spatial structure

3 x 32 x 32 image

unlike fully-connected layer

Convolve the filter with the image

slide over the image spatially, computing the dot products
Produces one number each dot product
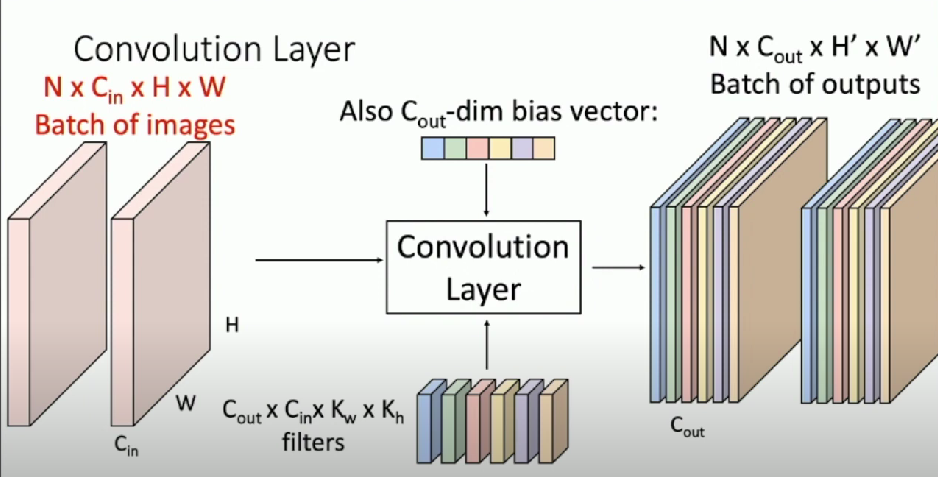
Filter always extend the full depth of the input volume

Pasted image 20241201224137.png

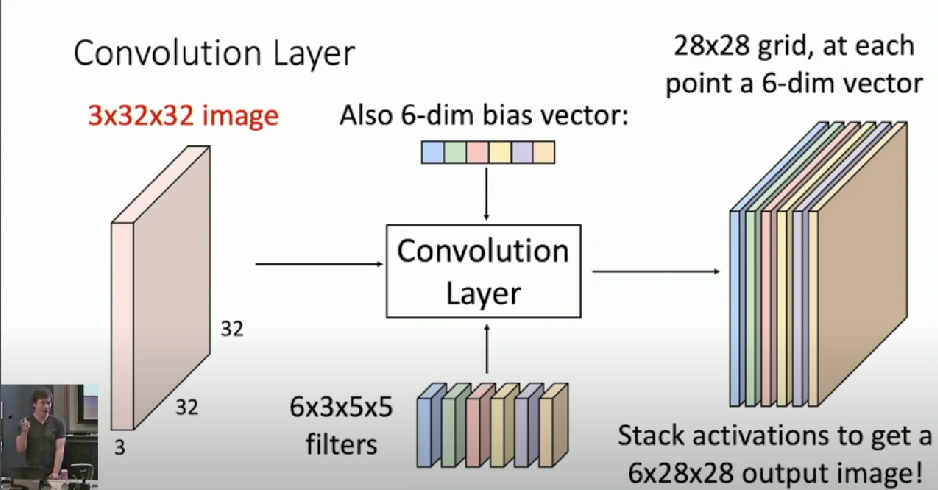
Number of filters is a Hyperparameters

6 filters in this case
There is also a bias for each filter

Often run on batch of images

Pasted image 20241201225611.png

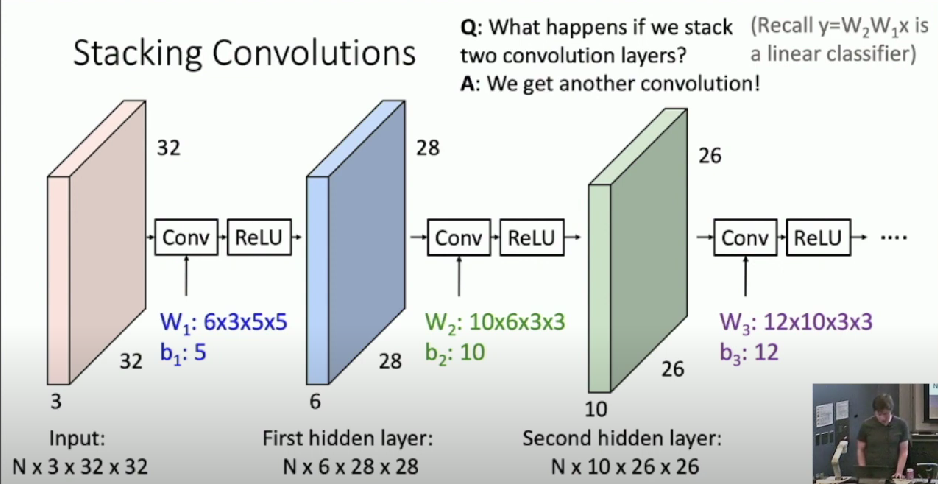
Stacking Convolutions

What if we stack two convolution layers?

We get another convolution!

Insert non-linear activation function between convolutional layers
Pasted image 20241201230640.png

What do convolutional filters learn?

First-layer conv filters: local image templates

often learns oriented edges, opposing colors

Closer look at spatial dimensions

How many times the filter can fit in the input

Input: W
Filter: K
Output: W - K + 1

Problem: Feature amps “shrink” with each layer!

Add padding around the input

Add zeros around the input
Input: W
Filter: K
Padding: P
Output: W - K + 1 + 2P

Common to set P=(K-1)/2 to make output have same size as input
Pasted image 20241201231618.png

Receptive Fields

For convolution with kernel size K, each element in the output depends on a K x K receptive field in the input

Each successive convolution adds K - 1 tot he receptive field size
With L layers the receptive field size is 1 + L * (K - 1)
Pasted image 20241201232042.png

For large images we need many layers for each output to “see” the whole image

Downsample inside the network

Strided Convolution

Stride is a Hyperparameters

Use filter on every stride to calculate dot product
Skip over some

Tldr

Input: W
Filter: K
Padding: P
Stride: S
Output: (W - K + 2P) / S + 1

Example

Input Volume: 3 x 32 x 32
10 5x5 filters with stride 1, pad 2

Output volume size: 10 x 32 x 32
(32 - 5 + 2 x 2) / 1 + 1 = 32 spatially, so 10 x 32 x 32

Number of learnable parameters: 760
Parameters per filter: 3 x 5 x 5 + 1 (bias) = 76
10 filters, so total is 10 x 76 = 760

Number of multiply-add operations: 768,000
10 x 32 x 32 = 10,240 outputs;
each output is the inner product of two 3 x 5 x 5 tensors (75 elements);
total = 75 x 10240 = 768,000

Hyperparameters

Kernel size
Number filters
Padding
Stride