3D Shape Representations

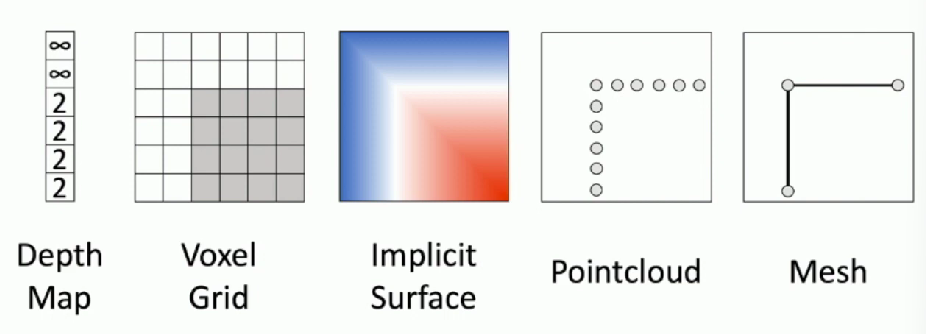
Pasted image 20241206173150.png

Depth Map

For each pixel, depth map gives distance from the camera to the object in the world at the pixel

RGB + Depth image = RGB-D Image (2.5D)
This type of data can be recorded directly for some types of 3D sensors

Pasted image 20241206173357.png

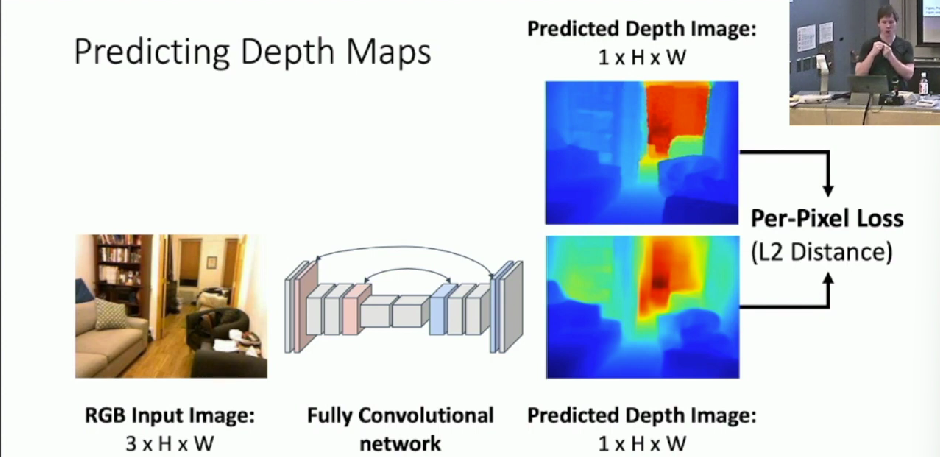
Predicting Depth Maps

Given an image, predict the depth map
We can use a fully convolutional network
Pasted image 20241206173552.png

Problem Scale / Depth Ambiguity

A small, close object looks exactly the same as a larger, farther-away object

Absolute scale / depth are ambiguous from a single image

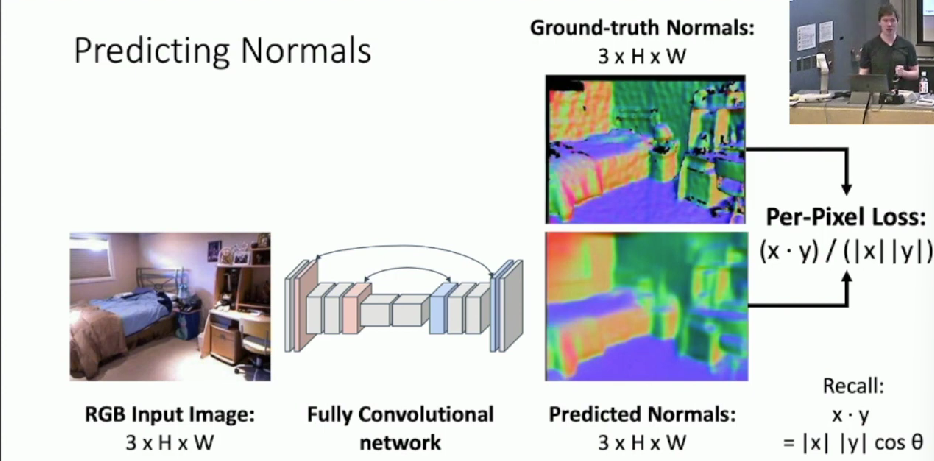
Surface Normals

For each pixel, surface normals give a vector giving the normal vector to the object in the world for that pixel

Pasted image 20241206174020.png

Predicting Normals

Similar to depth maps

Loss function is comparing angles between two vectors

Can predict depth map and normals with a single network

Voxel Grid

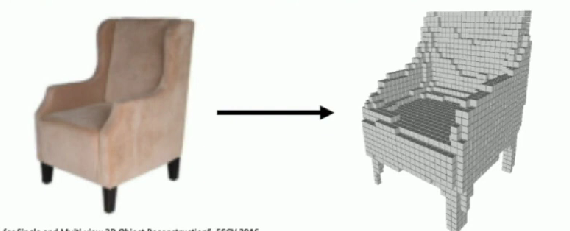
Pasted image 20241206174430.png

Represent a shape with a V x V x V grid of occupancies
Just like a segmentation masks in Instance Segmentation#Mask R-CNN, but in 3D

Conceptually simple: just a 3D grid

Need high spatial resolution to capture fine structures

Scaling to high resolutions is nontrivial

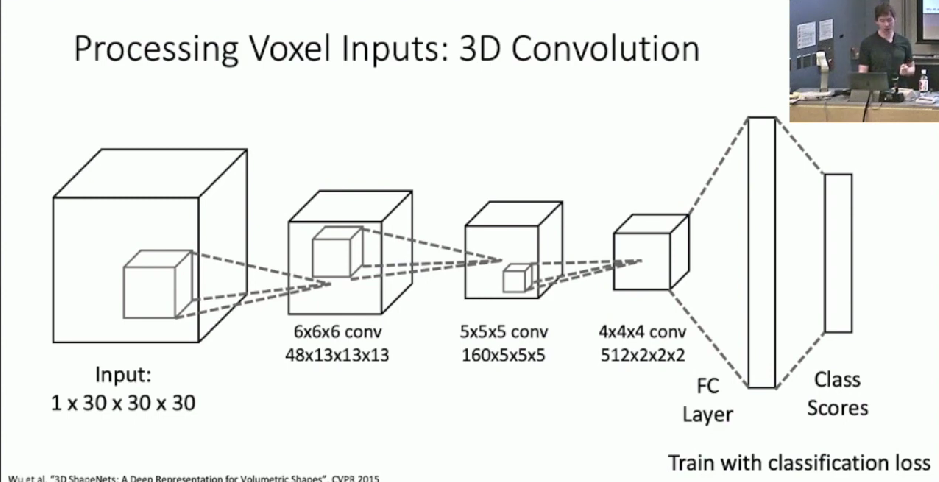
Processing Voxel Inputs: 3D Convolution

Kernel is 3D cube sliding through input

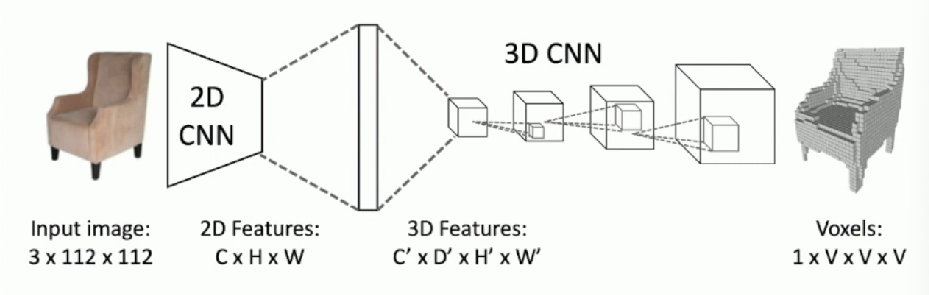
Generating Voxel Shapes: 3D Convolution

Pasted image 20241206182159.png

Voxel Problems: Memory Usage

Pasted image 20241206182905.png

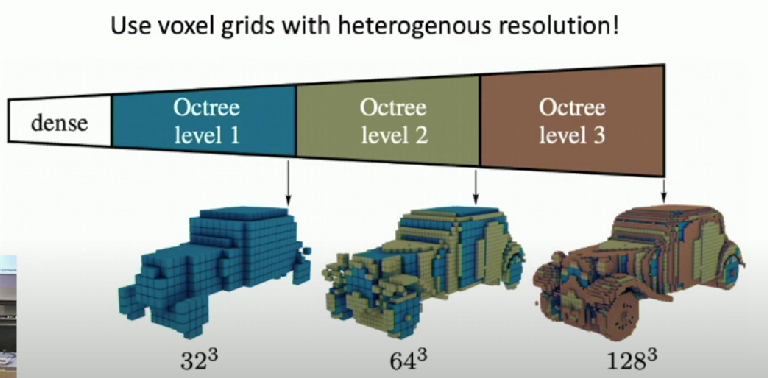
Scaling Voxels: Oct-Trees

Pasted image 20241206182940.png

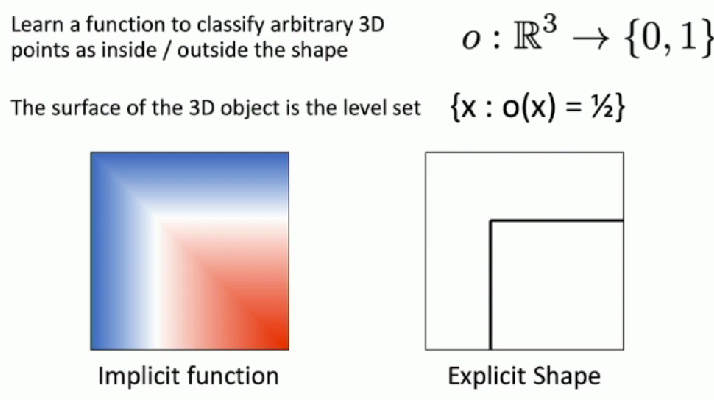
Implicit Functions

Learn a function to classify arbitrary 3D points as inside / outside the shape

The surface of the 3D object is the level set {x: o(x) = 1/2}
Pasted image 20241206183140.png
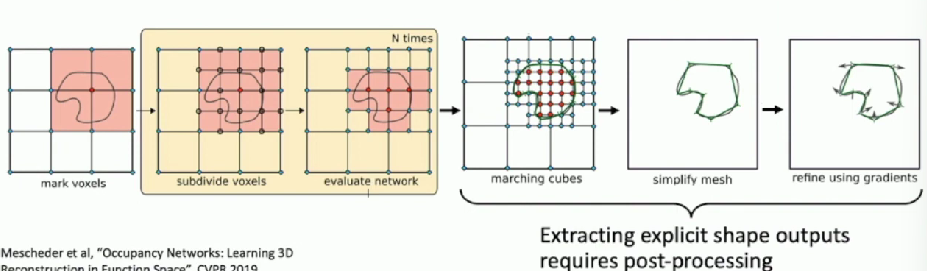
Pasted image 20241206183315.png

Point Cloud

Pasted image 20241206183519.png

Represent shape as a set of P points in 3D space
Requires new architecture, losses, etc

Can represent fine structures without huge numbers of points

Doesn’t explicitly represent the surface of the shape

Extracting a mesh for rendering or other applications requires post-processing

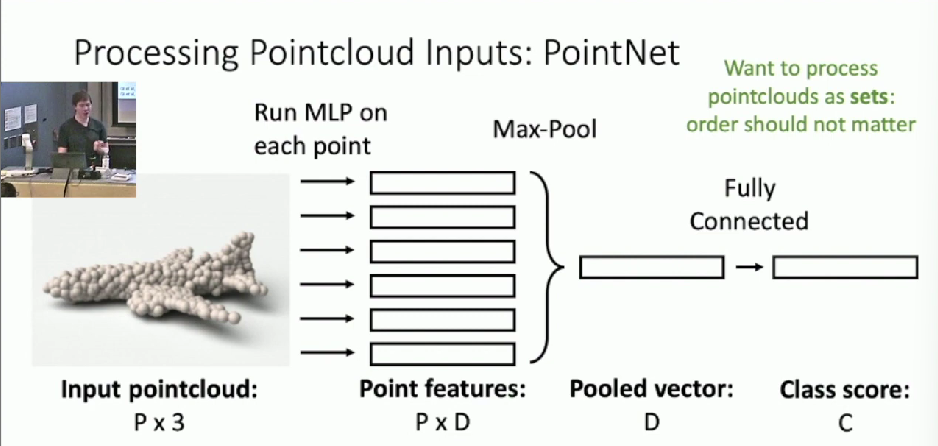
Processing Point Cloud Inputs: PointNet

Input: P points each with x, y, z positions

Order of points should not matter
Process pointclouds as set

Mesh

Triangle Mesh

Pasted image 20241206190502.png
Represent a 3D shape as a set of triangles
Vertices: Set of V points in 3D space
Faces: Set of triangles over the vertices

Benefits

Standard representation of graphics
Explicitly represents 3D shapes
Adaptive
- Can represent flat surfaces very efficiently
- Can allocate more faces to areas with fine details
Can attach data on verts and interpolate over the whole surface
- RGB colors, texture coordinates, normal vectors, etc

Problem

Nontrivial to process with neural networks