Floating Point Numbers

Floating Point Number Systems

Real Numbers

Infinite in extent
- There exists $x$ such that $| x |$ is arbitrarily large
Infinite in density
- Any interval $a \leq x \leq b$ contains infinitely many numbers

Standard Solution (Partial)

Floating point systems

An approximate representation of real numbers using a finite number of bits

Normalized Form of a Real number

After expressing the real number in the desired base $β$ , we multiply by a power of $p$ to shift it into a normalized form:

0. d_{1} d_{2} d_{3} d_{4} \dots \times β^{p}

where:

$d_{i}$ are digits in base $β$
normalized implies we shift to ensure $d_{1} \neq 0$
exponent $p$ is an integer
Density (or precision) is bounded by limiting the number of digits $t$
Extent (or range) is bounded by limiting the range of values for exponent $p$

Summary

$\pm 0. d_{1} d_{2} d_{3} d_{4} \dots d_{t} \times β^{p}$

for $L \leq p \leq U$ and $d_{1} \neq 0$

The four integer parameters ${β, t, L, U}$ characterize a specific floating point system, $F$ where $β =$ base, $t =$ mantissa, and $L$ and $U$ are the lower and upper bounds for the exponent.

Overflow / Underflow Errors

If the exponent is too big or too small, our system cannot represent this number
For underflow, answer rounds to 0
For overflow, will typically produce a $\pm \infty$ or NaN

Floating Point Standards

IEEE Single Precision (32 Bits): ${β = 2, t = 24, L = - 126, U = 127}$
IEEE Double Precision (64 Bits): ${β = 2, t = 53, L = - 1022, U = 1023}$

Floating Point Density

Floating point numbers are not evenly spaced

Rounding vs. Truncation

Round-to-nearest

Rounds to closest available number in $F$ .

Usually the default
We’ll break ties by simply rounding $\frac{1}{2}$ up

Truncation

Rounds to next number in $F$ towards 0.

Simply discard any digit after $t^{t h}$

Measuring Error

Difference between $x_{e x a c t}$ and $x_{b e t w e e n}$
We distinguish between absolute error and relative error.

E_{a b s} = | x_{e x a c t} - x_{a p p r o x} |

E_{r e l} = \frac{| x_{e x a c t} - x_{a p p r o x} |}{x_{e x a c t}}

Relative Error is often more useful

Is independent of the magnitudes of the numbers involved
Relates to the number of significant digits in the result

A result is correct to roughly $s$ digits if $E_{r e l} \approx 10^{- s}$ or

0.5 \times 10^{- s} \leq E_{r e l} \leq 5 \times 10^{- s}

Floating Point vs. Reals

For FP system $F$ , relative error between $X \in R$ , and its FP approximation, $f l (x)$ , has a bound, $E$

E_{r e l} = \frac{| x - f l (x) |}{x} ⟹ (1 - E) | x | \leq | f l (x) | \leq (1 + E) | x |

Machine Epsilon

The maximum relative error, $E$ , for a FP system is called machine epsilon or unit round-off error.
It is defined as the smallest value such that $f l (1 + E) > 1$ under the given floating point system.
We have the rule $f l (x) = x (1 + δ)$ for some $| δ | \leq E$ .
For an FP system ( $β, t, L, U$ ) with …

rounding to nearest: $E = \frac{1}{2} β^{1 - t}$
truncation: $E = β^{1 - t}$

Arithmetic with Floating Point

What guarantees are there on a FP arithmetic operation?

IEEE standard requires that for $w, x \in F$ :

w \oplus z = f l (w + x) = (w + z) (1 + δ)

This rule only applies to individual FP operations! Not sequences.

(a \oplus b) \oplus c \neq a \oplus (b \oplus c) \neq f l (a + b + c)

Result is order-dependent; associativity is broken!

Round-off Error Analysis

What can we say about $(a \oplus b) \oplus c$ ?

Let us use $E$ to give a bound on the relative error
$\begin{aligned} E_{r e l} & = \frac{| (a \oplus b) \oplus c - (a + b + c) |}{| a + b + c |} \\ = \frac{| [(a + b) (1 + δ_{1})] \oplus c - (a + b + c) |}{| a + b + c |} \\ = \frac{| [a + b + (a + b) δ_{1} + c] (1 + δ_{2}) - (a + b + c) |}{| a + b + c |} \\ = \frac{| (a + b) δ_{1} + (a + b + c + (a + b) δ_{1}) δ_{2} |}{| a + b + c |} \\ = \frac{| (a + b) δ_{1} + (a + b + c) δ_{2} + (a + b) δ_{1} δ_{2} |}{| a + b + c |} \\ \leq \frac{| (a + b) δ_{1} | + | (a + b + c) δ_{2} | + | (a + b) δ_{1} δ_{2} |}{| a + b + c |} \\ \leq \frac{| (a + b) | E + | (a + b + c) | E + | (a + b) | E^{2}}{| a + b + c |} \\ \leq \frac{| a | + | b | + | c |}{| a + b + c |} (2 E + E^{2}) \end{aligned}$
This analysis describes only the worst case error magnification. Actual error could be much less.

Behaviour of Error Bounds

We showed that $(a \oplus b) \oplus c$ satisfies:

E_{r e l} \leq \frac{| a | + | b | + | c |}{| a + b + c |} (2 E + E^{2})

The term $\frac{| a | + | b | + | c |}{| a + b + c |}$ describes how much $E$ could be scaled by to give the total error, when summing 3 numbers $a, b, c$ .

Cancellation Errors

When is $\frac{| a | + | b | + | c |}{| a + b + c |}$ large?

when $| a + b + c | ≪ | a | + | b | + | c |$
this occurs when quantities have differing signs and similar magnitudes

Expressions without cancellation often have better bounds on error

Catastrophic cancellation occurs when subtracting numbers about the same magnitude, when the input numbers contain error.

All significant digits may cancel out.

Stability of Algorithms

If any initial error in the data is magnified by an algorithm, the algorithm is considered numerically unstable.

Conditioning of Problems

For problem $P$ , with input $I$ and output $O$ , if a change to the input, $Δ I$ , gives a small change in the output $Δ O$ , $P$ , is well-conditioned. Otherwise, $P$ is ill-conditioned.

This is a property of the problem itself, independent of any specific implementation.

Geometric Example

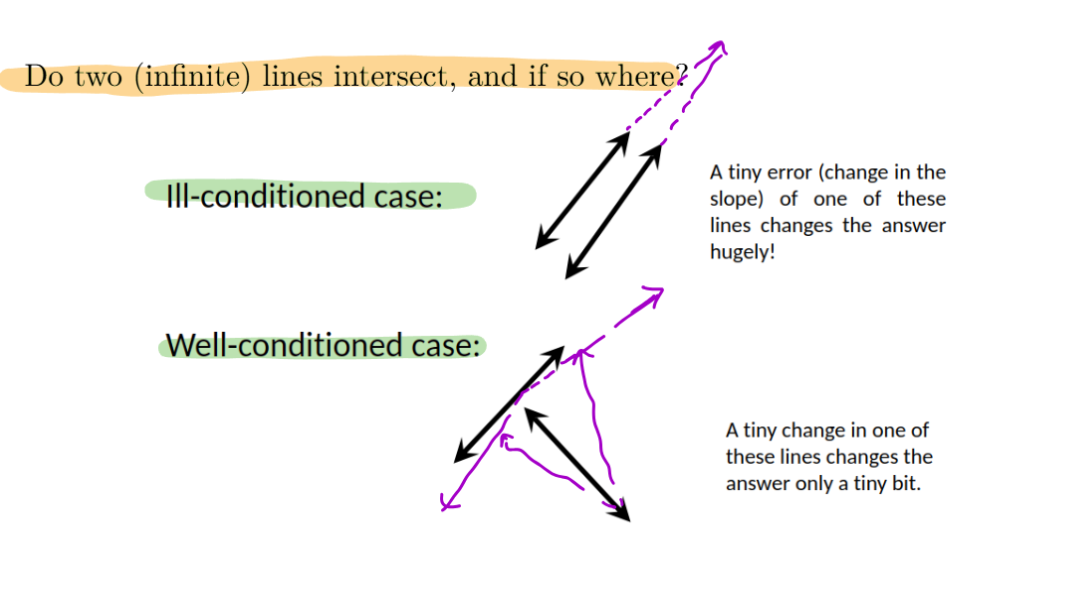
Pasted image 20250302174833.png

Conditioning vs. Stability

Conditioning of a problem:

How sensitive is the problem itself to errors or changes in input?
Stability of a numerical algorithm:
How sensitive is the algorithm to errors or changes in input?
Note that:

An algorithm can be unstable even for a well-conditioned problem!
An ill-conditioned problem limits how well we can expect any algorithm to perform

Stability Analysis of an Algorithm

We can analyse whether errors accumulate or shrink to determine the stability of algorithms

Example

Pasted image 20250302201723.png

Floating Point Numbers